薛定谔波动方程:推导和解释| Electrical4Ubetway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

薛定谔方程是什么?

的薛定谔方程(也称为薛定谔波动方程)是一个偏微分方程描述量子力学系统的动力学通过波函数。轨迹、定位和这些系统的能量可以通过求解薛定谔方程中检索。

亚原子粒子是编码的所有信息在一个波函数。波函数满足,可以用薛定谔方程来解决。薛定谔方程的基本原理,介绍了大学物理。也愈发常见电气工程中的薛定谔方程引入适用于高校教学大纲必威电竞赞助半导体。

不幸的是,它只是说作为一个假设在这两种情况下,从未在任何有意义的方式。这是相当不满的几乎一切教本科量子物理是建立在这个基础之上的。在本文中,我们将从头推导出方程,我会尽我所能显示每一步。

有趣的是,参数我们将同那些被薛定谔自己所以你可以看到思考一个巨大的线是在他的时间。提醒一下,这里是三维的含时薛定谔方程(非相对论粒子)在所有它的美:

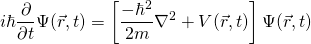
量子物理学和海浪

每个人都喜欢包经典物理学——但它很好地为我们服务一段时间(认为牛顿力学、麦克斯韦方程和狭义相对论)。

然而,如我们先前的文章所示,实验结果在世纪之交的时候没有太华丽相比已知的物理学。我们的文章双缝实验和在某种程度上光电效应实验结果不匹配与已知的对时间的理解。

但是为什么呢?简而言之,在经典物理存在两个实体,粒子和波。这两个实体的特征可以描述如下:

粒子:本地化包质量的能量和动量 $米$ 。

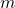波:干扰分布在用。他们可以用一个波函数描述 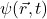$vec {\ psi (\ r}, t)$ 描述波在空间和时间。

这给我们带来了令人惊讶的结果发现在我们光电发射篇文章。我们发现电子显示这两个这些属性。这完全与已知的对时间的理解两个实体被认为是相互排斥的。

疯狂对吧?大约就在这个时候,一些非常有影响力的人物在物理知识,开始意识到有一个缺口,一个大突破是当路易德布罗意相关的动量(粒子)一个波长(波)

$开始\ p{方程*}= h / \λ。结束\{方程*}$

另外,从光电发射我们知道,能量吸收和发射的光子(仍然不确定粒子或波)能量由:

$\{方程*}开始E =高频结束=ω\百巴\ \{方程*}$

在哪里 $\百巴= h / 2 \π$ 和 $\ω= 2π\ f$ 。我们现在在同一阶段薛定谔推导之前他著名的方程。但我们在哪里开始?嗯,我们知道电子和光子表现出波动性和粒子的行为。不会有什么毛病开始普遍方程,所有波应该服从,然后引入粒子物理上是否有结果。

如何得到波动方程

干扰 $vec {\ psi (\ r}, t)$ 遵循波方程。记住,电子衍射,显示有一个电磁充电。因此,现在,让我们看看电磁场。在这种情况下,麦克斯韦方程应用和它们在所有的荣耀。

${对齐*}\微分算符\ \开始vec {E} & = - * \ \压裂{\部分{\ vec {B}}}{\部分{t}} \ \ \微分算符\ vec {B} & = - * \ \ mu_0 \离开vec {J} + (\ \ epsilon_0 \压裂{\部分{\ vec {E}}}{\部分{t}} \) \ \ \微分算符\ cdot vec {E} & = \ \压裂{\ρ}{\ epsilon_0} \ \ \微分算符\ cdot vec {B} & = 0 \ \{对齐*}结束$

在哪里 $c$ 光速在真空中, $vec {E} \$ 电场和吗 $vec {B} \$ 是磁场。第一个方程是发电机的基础之上,电感,变压器和法拉第定律的化身。

同时,的意义之一 $vec {B} \微分算符\ cdot \ = 0$ 是,不存在磁单极子。理解这些方程的推导和背后的物理意义是一个全面的工程师。现在,让我们得到任何电磁波方程必须服从通过应用一个旋度方程4:

${对齐*}\微分算符\ \开始vec {E} & = - * \ \压裂{\部分{\ vec {B}}}{\部分{t}} \ \ \意味着\微分算符\ * (vec {E} \ \微分算符\倍)& = - \压裂{\部分{(vec {B} \ \微分算符\倍)}}{\部分{t}} \ \ \意味着\微分算符\ * (vec {E} \ \微分算符\倍)& = - \压裂{1}{c ^ 2} \压裂{\部分^ 2 {\ vec {E}}}{\部分{t ^ 2}}{对齐*}\结束$

现在我们可以利用一个非常熟悉和容易证明向量标识: $(\ \微分算符\次微分算符\ * T) = \微分算符(\微分算符\ cdot T) - \微分算符^ 2 T$ 在哪里 $T$ 是一些占位符向量。申请我们的小方程:

$\开始{对齐*}\微分算符(\微分算符\ cdot \ vec {E}) - \微分算符^ vec {E} & = - 2 \ \压裂{1}{c ^ 2} \压裂{\部分^ 2 {\ vec {E}}}{\部分{t ^ 2}} \ \ \暗示——\微分算符^ vec {E} & = - 2 \ \压裂{1}{c ^ 2} \压裂{\部分^ 2 {\ vec {E}}}{\部分{t ^ 2}} \ \ \微分算符vec {E} - ^ 2 \ \压裂{1}{c ^ 2} \压裂{\部分^ 2 {\ vec {E}}}{\部分{t ^ 2}} & = 0结束\{对齐*}$

结果我们在三维电磁波动方程。这个方程不仅体现为一种电磁波,但也显示了音响、地震波,声波,水波,流体动力学。

如何推导出薛定谔方程

平面波波动方程的解决方案

从一维波动方程(很容易推广三维之后,将适用于所有的逻辑 $x, y$ , $z$ 维度。):

${方程*}\ \开始压裂{{\部分^ 2 {E}}}{\部分^ 2 {x}} = \压裂{1}{c ^ 2} \压裂{{\部分^ 2 {E}}}{\部分^ 2 {t}} \ Longrightarrow \压裂{{\部分^ 2 {E}}}{\部分^ 2 {x}} - \压裂{1}{c ^ 2} \压裂{{\部分^ 2 {E}}}{\部分^ 2 {t}} = 0 \{方程*}结束$

在现实中,这是一个二阶偏微分方程和平面波的解决方案感到满意:

$\{方程*}开始E (x, t) = E_0 E ^{我(kx - \ωt)}{\文本(检查这自己!)。}\结束{方程*}$

我们从正常的波动力学知道在哪里 $k = \压裂{2 \π}{\λ}$ 和 $\ω= 2π\ f$ 。现在,让我们使用的工作从爱因斯坦和康普顿和替代,一个光子的能量是由 $\ mathsf {E} = \百巴\ω$ 和德布罗意, $p = h / \λ= \百巴k$ 。我们可以进一步的按摩平面波解:

$\{方程*}开始E (x, t) = E_0 E ^{\压裂{我}{\百巴}(px - \ mathsf {E} t)} \{方程*}结束$

这是平面波方程描述一个光子。让我们把这个方程代入波动方程看看我们发现!

$左(\ \开始{对齐*}\压裂{{\部分^ 2{}}}{\部分^ 2 {x}} - \压裂{1}{c ^ 2} \压裂{{\部分^ 2{}}}{\部分^ 2 {t}} \右)E_0 e ^{\压裂{我}{\百巴}(px - \ mathsf {e} t)} & = 0 \ \ \暗示——\压裂{1}{\百巴^ 2}\离开(p ^ 2 - \压裂{\ mathsf {e} ^ 2} {c ^ 2} \右)E_0 e ^{\压裂{我}{\百巴}(px - \ mathsf {e} t)} & = 0结束\{对齐*}$

换句话说, $\ mathsf {E} ^ 2 = p c ^ 2 ^ 2$ 这是伟大的,因为我们从狭义相对论,相对论性粒子的总能量与质量 $米$ 是:

${方程*}\ \开始mathsf {E} ^ 2 = p c ^ 2 ^ 2 + m ^ 2 c ^ 4 \{方程*}结束$

我们只处理光子到目前为止没有质量 $(m = 0)$ !让我们扩大我们的理解和应用总相对论能量粒子的质量(例如电子)和改变我们的方程的名字 $\ψ$ 因为我们没有超大。

$\{方程*}-开始\压裂{1}{\百巴^ 2}\离开(p ^ 2 - \压裂{\ mathsf {E} ^ 2} {c ^ 2} + m ^ 2 c ^ 2 \) \ Psi E ^{\压裂{我}{\百巴}(px - \ mathsf {E} t)} = 0结束\{方程*}$

现在这个方程直接来自用平面波方程代替一个光子波动方程。然而,由于我们现在希望能源解决总相对论能量粒子的质量,我们需要改变略有波动方程。这是因为波动方程不能完全适用于我们的新 $\ψ$ 用于描述粒子和波。我们现在可以backsolve经营者得到上面的方程,给出了:

$左(\ \开始{方程*}\压裂{{\部分^ 2{}}}{\部分^ 2 {x}} - \压裂{1}{c ^ 2} \压裂{{\部分^ 2{}}}{\部分^ 2 {t}} - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}\)\ Psi e ^{\压裂{我}{\百巴}(px - \ mathsf {e} t)} = 0结束\{方程*}$

波动方程求解粒子以质量

我们现在想做一些近似的全部能源我们所描述的 $\ mathsf {E}$ 为一个粒子动量和质量。让我们重新排列公式略我们可以使用一些近似。

${对齐*}\ \开始mathsf {E} ^ 2 & = p c ^ 2 ^ 2 + m ^ 2 c ^ 4 \ \ \ mathsf {E} & = \√6{\离开(p c ^ 2 ^ 2 + m ^ 2 c ^ 4 \右)}\ \ & = \√6{\离开(c ^ 4(\压裂{p ^ 2} {c ^ 2} + m ^ 2) \右)}\ \ & = \√6{\离开(c ^ 4 m ^ 2(\压裂{p ^ 2} {m ^ 2 c ^ 2} + 1) \右)}\ \ & = mc ^ 2 \√{\离开(\压裂{p ^ 2} {m ^ 2 c ^ 2} + 1 \右)}\{对齐*}结束$

这个操作的目的是得到的方程形式 $\ sqrt {1 + x}$ 因为如果我们把这个方程得到的泰勒级数展开:

${方程*}\ \开始sqrt {1 + x} \大约1 + \压裂{x}{2} - \压裂{x ^ 2}{8} + \压裂{x ^ 3} {16} +……结束\{方程*}$

当 $x$ 很小,泰勒展开式中,剩下的只有一部分是吗 $O (1)$ 术语。在我们的能量公式, $x = \压裂{p ^ 2} {m ^ 2 c ^ 2} = \离开(\压裂{p} {mc} \右)^ 2$ 。我们可以利用这一事实 $p = mv \ mc$ 对于任何不以光速旅行(请找我如果你发现任何不满足这个)!所以这个词实际上减少了:

$\开始{对齐*}\ mathsf {E} & = mc ^ 2 \√{\离开(\压裂{p ^ 2} {m ^ 2 c ^ 2} + 1 \右)}\ \ & \大约mc ^ 2 \离开(1 + \压裂{1}{2}\压裂{p ^ 2} {m ^ 2 c ^ 2} \) \ \ & = mc ^ 2 + \压裂{p ^ 2} {2 m} = mc ^ 2 + E_{\文本{动能}}{对齐*}\结束$

在哪里

$文本\{方程*}E_开始\{动能}= \压裂{1}{2}mv ^ 2 = \压裂{1}{2}\压裂{(mv) ^ 2} {m} = \压裂{p ^ 2} {2 m} \{方程*}结束$

是正常的动能,我们看到从高中物理。现在回到之前的波函数,现在让我们输入这个新信息,看看我们得到:

$\开始{对齐*}\ Psi (vec {r} \ t) & = \ Psi_0 e ^{\压裂{我}{\百巴}(vec {r} - p \ \ mathsf {e} t)} \ \ & = \ Psi_0 e ^{\压裂{我}{\百巴}(p vec {r} \ - mc ^ 2 t - E_{\文本{动能}}t)} \ \ & ^ = e{- \压裂{我}{\百巴}mc ^ 2 t} \ Psi_0 e ^{\压裂{我}{\百巴}vec {r} - E_ (p \{\文本{动能}}t)} \ \ \{对齐*}结束$

我们已经把两项的原因是,第一项 $e ^{- \压裂{我}{\百巴}mc ^ 2 t}$ (再次基于光速)将振荡明显多于第二项和不一定描述波粒实体后。为了巩固这种差异,让我们建立:

${方程*}\ \开始Psi (vec {r} \ t) = e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ Psi (vec {r} \ t) \{方程*}结束$

我们现在定义:

${方程*}\ \开始psi (vec {r} \ t) = \ Psi_0 e ^{\压裂{我}{\百巴}vec {r} - E_ (p \{\文本{动能}}t)}。结束\{方程*}$

现在让我们把第一和第二部分的衍生品 $vec {\ Psi (\ r}, t)$ 看看我们最终得到的。第一个:

${方程*}\ \开始压裂{\部分{\ Psi}}{\部分t} = - \压裂{我}{\百巴}mc ^ 2 e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ Psi (vec {r} \ t) + e ^{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ Psi (vec {r} \ t)}{\部分t} \{方程*}结束$

第二个:

$\开始{方程*}\压裂{\部分^ 2 {\ Psi}}{\部分t ^ 2} = \离开(- \压裂{m ^ 2 c ^ 4}{\百巴^ 2}e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ Psi - \压裂我{2}{\百巴}mc ^ ^ 2 e{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ Psi}{\部分t} \右)+ e ^{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分^ 2 \ Psi}{\部分t ^ 2} \{方程*}结束$

我们应该记住,上学期第二次偏导数很小,因为没有这一事实 $c ^ 2$ 词携带数量级,因此通过近似,给出了实际的二阶导数:

$\开始{对齐*}\压裂{\部分^ 2 {\ Psi}}{\部分t ^ 2} \大约\离开(- \压裂{m ^ 2 c ^ 4}{\百巴^ 2}e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ Psi - \压裂我{2}{\百巴}mc ^ ^ 2 e{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ Psi}{\部分t} \) \{对齐*}结束$

卑鄙的原因我们把这两个偏导数,这样我们可以转嫁到这个方程描述了波函数之前:

但在我们能做到这一点,让我们重新安排这个公式,我们最终会得到一个方程称为克莱因-戈登方程:

$左(\ \开始{对齐*}\压裂{{\部分^ 2{}}}{\部分^ 2 {x}} - \压裂{1}{c ^ 2} \压裂{{\部分^ 2{}}}{\部分^ 2 {t}} - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}\)\ Psi_0 e ^{\压裂{我}{\百巴}(px - \ mathsf {e} t)} & = 0 \ \ \压裂{{\部分^ 2 {\ Psi (x, t)}}}{\部分^ 2 {x}} - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}\ Psi (x, t) & = \压裂{1}{c ^ 2} \压裂{{\部分^ 2 {\ Psi (x, t)}}}{\部分^ 2 {t}} \{对齐*}结束$

现在我们可以很容易地推广到三维将方程转化为矢量方程(所有我们采取的措施是将申请所有推导公式 $x, y$ , $z$ 。)

$\开始{方程*}\微分算符^ 2 \ Psi (vec {r} \ t) - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}\ Psi (vec {r} \ t) = \压裂{1}{c ^ 2} \压裂{{\部分^ 2 {\ Psi (vec {r} \ t)}}}{\部分^ 2 {t}} \{方程*}结束$

这个方程被称为克莱因-戈登方程自由粒子。这个方程是相对论的能量项并不能让我们的小的假设 $\ sqrt {1 + x}$ 泰勒展开式。

现在,让我们来简化克莱因-戈登方程(回溯到一维和应用我们的新能量公式),我们会到达期待已久的薛定谔方程:

${对齐*}\ \开始压裂{{\部分^ 2 {\ Psi}}}{\部分^ 2 {x}} - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}\ Psi & = \压裂{1}{c ^ 2} \压裂{{\部分^ 2 {\ Psi}}}{\部分^ 2 {t}} \{对齐*}结束$

让我们把我们的新波函数给出的 $\ Psi (vec {r} \ t) = e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ Psi (vec {r} \ t)$ 我们知道这个对时间的一阶和二阶导数的样子:

$\开始{对齐*}\压裂{{\部分^ 2{}}}{\部分^ 2 {x}} e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi & = \压裂{1}{c ^ 2} \离开(- \压裂{m ^ 2 c ^ 4}{\百巴^ 2}e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi - \压裂我{2}{\百巴}mc ^ ^ 2 e{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ psi}{\部分t} \右)+ e ^{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ psi}{\部分t} \ \ \压裂{{\部分^ 2{}}}{\部分^ 2 {x}} e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi & = \压裂{m ^ 2 c ^ 2}{\百巴^ 2}e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi - \压裂{m ^ 2 c ^ 2}{\百巴^ 2}e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi - \压裂我{2}{\百巴}我^{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ psi}{\部分t} + e ^{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分^ 2 \ psi}{\部分t ^ 2} \ \ \压裂{{\部分^ 2{}}}{\部分^ 2 {x}} e ^{- \压裂{我}{\百巴}mc ^ 2 t} \ psi & = - \压裂我{2}{\百巴}我^{- \压裂{我}{\百巴}mc ^ 2 t} \压裂{\部分\ psi}{\部分t} \ \ e ^{- \压裂{我}{\百巴}mc ^ 2 t} \离开(\压裂{{\部分^ 2 {\ psi}}}{\部分^ 2 {x}} + \压裂{2 im}{\百巴}\压裂{\部分\ psi}{\部分t} \右)& = 0结束\{对齐*}$

现在我们需要做的就是一个简单的重新排列得到薛定谔方程在三维空间中(注意 $\压裂{1}{我}=我$ ):

$\{方程*}我开始\百巴\压裂{\部分{}}{\部分{t}} \ Psi (vec {r} \ t) = \压裂{- \百巴^ 2}{2 m} \微分算符^ 2 \ Psi (vec {r} \ t)结束\{方程*}$

的参数可以通过注意的相似的经典哈密顿项右边的方程描述了波函数的总能量。

在推导过程中,我们假设 $V (vec {r} \ t)$ 是0,只考虑动能。我们知道可能是纯粹的添加剂对其空间变异,因此,完整的薛定谔方程在三维空间与潜力是由:

$\{方程*}我开始\百巴\压裂{\部分{}}{\部分{t}} \ Psi (vec {r} \ t) =左\[\压裂{- \百巴^ 2}{2 m} \微分算符^ 2 + V (vec {r} \ t)正确\]\ Psi (vec {r} \ t)。结束\{方程*}$

就是这样!我们拥有它,本文推导出完整的薛定谔方程的非相对论粒子在三维空间中。如果你喜欢这篇文章,希望看到更多,请电子邮件我们,让我们知道。

引用

Gasiorowicz,美国(2019年)。量子物理学。第二版。加拿大:汉密尔顿印刷、pp.1-50。
格里菲思,d . (2019)。量子物理学。第三。大学印刷厂,剑桥:剑桥大学出版社。
病房里,d . Volkmer,美国(2019年)。如何推导出薛定谔方程。[网络]arXiv.org。可以在https://arxiv.org/abs/physics/0610121v1(2019年5月29日通过)。
Shankar r (1980)。量子力学原理。第1版。纽约:科学,pp.1-40施普林格。

薛定谔波动方程:推导和解释