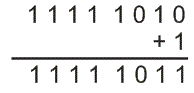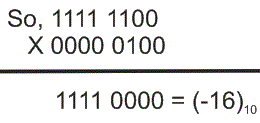2的补有一个有趣的性质吗二进制算术操作可以很容易地对有符号或无符号的数字进行。它的结果是正确的2的补码。
如何表示2的补码中的十进制数?
我们来计算一下。负号是这个数和这个数的和是零。以我们最熟悉的十进制数制为例。
在那里,
在二进制中只有两位数字0和1。在双星系统每一个数字和它的符号都只用0和1这两个数字来表示。由于正负符号不能直接用二进位表示,我们必须找到另一种表示它们的方法。
为此,我们利用了负数的定义。如果我们要表示一个负的二进制数,我们必须找到一个二进制数和原始的无符号或正二进制数是零。由于这两个数的和为零,所以取第二个数作为第一个数的负等价物。
假设我们要把- 5写成二进制也就是- 5或+ 5。现在5或+ 5可以用二进制或8位系统表示为0000 0101,0在二进制或8位系统中表示为0000 0000。
因此这个结果是(- 5)的表示10.
现在让我们研究一下2的补0000 0101,这是
因此,我们证明了0减去任何二进制数都是这个数的2的补数,因此2是任何数的2的补数二进制数可以表示为这个数的负等价物。在2的补码中,首先将一个十进制数转换为二进制数。假设我们要表示(5)10二进制的2的补码。(5)的二进制表示100101 (0000)2.
有趣的是无符号形式(5)10(5)的二进制形式直接表示为2的补码。10例如(0000 0101)2.无符号数作为正数处理。有符号的小数可以是正数也可以是负数。现在计算2的补对于有符号的十进制数,如(-5)10,我们必须找出1的补然后把每一个数字转换成它的对边数字(即1转换成0或0转换成1),最后加1。这个加后的结果是2的有符号(负)小数的完整表示。
现在看看下面的图表。
(+ 5)10等于(5)10.但对于(1)10它被视为无符号(255)10.(5)10⇔(251)10
记住- 2的补数总是表示为二进制数,这样当和一个相同大小的正数相加时一定是零。
重要的是要记住最左位或有效位表示整数的符号。它也被称为有符号位。
- 如果最左边的位是零,那么这个数就是正的。
- 如果最左边的位是1,那么这个数就是负数。
2的补码算法
2的补码之外
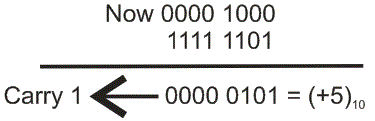
2的补码的加法,它总是遵循与正常情况下相同的规则二进制加法.假设我们要加上(8)10和(3)10.
首先我们要把它们转换成2的补然后把它们相加。
如果进位是1,那么number就是正的。这里进位是1,它是8位的,因此不考虑字节,因此答案是一个字节长的正数。所以很明显,对于有符号数和无符号数,加法可以在2的补码中很容易地进行。
2的补减法
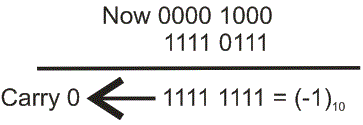
2的补码中的减法与一般的二进制加法中的减法遵循相同的规则。唯一的问题是,这里的减法首先转化为负数然后加上被减数。假设减去(8)10从(9)10.第一次转换(8)10从(9)10放入2的补码,然后简单相加。
如果进位是0,那么number就是负数。所以很明显,减法可以很容易地在2的补很容易。
2的补码乘法
对于2的补乘,它总是遵循相同的规则二进制乘法.假设我们要乘以(- 4)10(4)10出(-16)10.现在(- 4)10= 1111 1100在2的补码和(4)10= 0000 0100在2的补码中
2的补师
对于2的补数除法,方法是重复2的补数减法。首先计算除数的2的补数,然后将这个转换后的除数加到被除数中。现在进入下一个减法循环。这里商代替了被除数。一遍又一遍地重复,直到商变小或为零。如果不为零,则视为余数。假设我们要计算(7)10÷(3)10答案(2)10商和(1)10剩余部分。现在我们开始计算它2的补.
由于重复是两轮,那么商是(2)10.