补码系统
数字系统中的补码表示该数字与该数字的最高数字之间的差值。这个定义可以应用于各种数字系统,它们的命名也不同。但一般来说,如果一个数字的基数是N,那么这就是(N-1)的补码。然而,如果我们加上一个值,就会得到N的补码。例如,让我们从十进制数开始,因为我们基本上熟悉那个数字系统。让我们乘25路车。补码可以通过两种方式找到,因为它的基数是10,称为(10-1),也就是说9的补.
方法1:第一种方法是用数字中最大的数减去数字,这意味着99要减去数字。得到(99 - 25)= 74。
方法2:在第二种方法中,每个数字被单独考虑并从9中减去,因为9是最高的。所以我们得到了9-2,9-5,这意味着答案是74。因此,我们得到了相同的答案,两种求补的方法都是正确的,可以根据我们的意愿应用。
二进制数系统:现在来到一个二进制数这是我们讨论的主要话题。它只有两个数字0和1,因此名称是二进制的。它的基数是2,所以如果我们从这个数字的最高数字中减去它,我们得到(2–1),也就是说1的补. 如果将1与之相加,我们将得到2的补码。同样,如果单个数字从1中减去(0和1之间的最高值),那么我们也会得到1的补码,加上1,我们会得到2的补语. 然而,幸运的是,还有另一种方法可以找到1的补码。我们不必记住所有这些步骤来找出1和2的补码,但一个简单的技巧就可以完成这项工作。
我们前面讨论过的两种方法是相似的,但我们可以使用一种新的方法或技巧来求1的补数。让我们打破悬念,看看各种方法,找出1和2的补语举个例子。例如,我们必须找出0100的2的补码。在这里,数字之前使用了零,使其成为四位数字。因为,对于二进制系统,我们有2次幂的位数。
方法- 1在这种方法中,我们必须用1111减去它,因为它是最大的四位数1的补. 1111–0100是1011。2的补码是1011+1,也就是1100。
方法- 2这里,从1中减去每一个数字就得到1的补.结果是1 - 0,1 - 1,1 - 0,1 - 0,1 - 0,即1011。
2的补语是1011 + 1 = 1100。
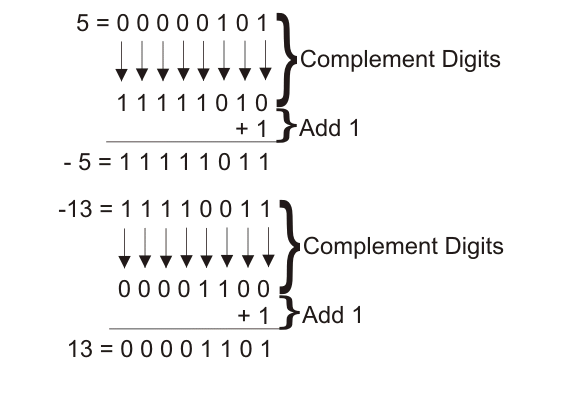
方法- 3在这里,我们必须用0替换1,用1替换0,以找出1的补码。用这个结果加上一个将得到2的补码。
对于0100,我们只需将1替换为0,将0替换为1,就可以得到结果1011。用这个结果加1将得到(1011+1),也就是1100。
因此,在这三种方法中,我们都发现了相同的结果,所有的方法都是正确的,人们可以根据其方便性使用其中的任何一种。
正数和负数的补码表示。
为什么我们需要2的补码?
使用的主要问题2的补语它可以用于两个二进制数字的减法运算。正如我们所知道的那样,计算机只懂二进制,而在计算机中没有所谓的负数二进制但绝对有必要使用二进制表示负数,这可以通过将符号位分配给需要额外位的数字来完成。如果符号位为1,则该数字被视为负数,如果为0,则该数字将被称为正数。
对于二进制数的减法,可以这样做-
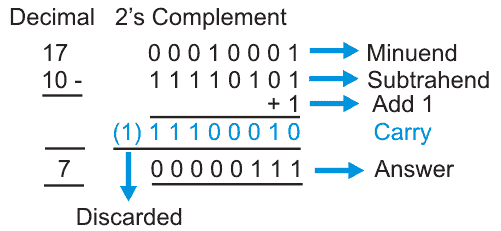
从较大的数字中减去较小的数字
- 求较小数的2的补数。
- 把大的数和小的数的补数相加。
- 丢弃的。
- 放弃进位后,保留将作为减法答案的结果。
从较小的数中减去较大的数
- 找到较大数的2的补码。
- 将较大数字的2的补码加到较小数字上。
- 如果未生成进位,则查找结果的2的补码,结果将为负数。
- 如果生成进位,则放弃进位并获取结果,结果将为答案,符号将为负数。
用较小的数减去较大的数。
2的补码的优点
- 减法可以借助于2的补码法来完成。
- 易于实现与更大的电路。
- 端回携带不需要像在以下情况下那样执行:1的补.
- 负数可以用2的补语.