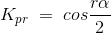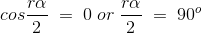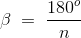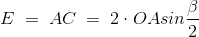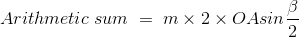在知道之前,蜿蜒的因素,我们应该知道距的因素和分布的因素, 自从蜿蜒的因素是产品的距的因素和分布的因素.
如果我们用K表示缠绕因子w, pitch factor with Kp和K的分布因子d,我们可以写
的距的因素和分布的因素下文逐一解释。
距的因素
在短频带线圈中,线圈两侧的感应电动势矢量相加,得到线圈的合成电动势。在短节线圈中,相对线圈两侧的感应电动势之间的相位角小于180o(电)。但我们知道,在全频带线圈中,线圈两侧感应电动势之间的相位角正好是180o(电)。
因此,全螺距线圈的电动势就是线圈两侧感应电动势的算术和。我们很清楚两个量的矢量和或相量和总是小于它们的算术和。节距因数是短节距线圈的合电动势与全节距线圈的合电动势的比较的量度。
因此,它必须是每个线圈的感应电动势的相量和与每个线圈的感应电动势的算术和之比。因此,它必须小于统一。
让我们假设,一个线圈是短的角度α(电度)。每侧线圈感应电动势为e,感应电动势的算术和为2E。也就是说,2E是诱导的电压穿过线圈端子,如果线圈已经完全倾斜。
现在,来到短倾斜线圈。从下图中,清楚的是,短倾斜线圈的结果EMF
现在,按照倾斜因子的定义,
这种音调因子是EMF的基本组成部分。的助势波可能包括空间场谐波在产生的电压波形中也会产生相应的时间谐波。一个3理查德·道金斯磁通波的谐波分量可以想象为由三个极点产生,而基波分量则是由一个极点产生。
鉴于此,R的弦角th谐波变成了r的基本组件和音调因子的弦角th谐波是,
r.th谐波变为零,如果,
在三相交流发电机中,3理查德·道金斯在三相变压器的情况下,通过星形或三角形连接来抑制谐波。在设计一个3阶段时给予了全部的注意交流发电机绕线设计,适用于5th和7th谐波。
5th谐波
7th谐波
因此,采用合适的弦合角α = 30o,我们做最优化的设计交流发电机的衔接绕组.
分布的因素
如果在一个杆下方的任何一个相的线圈侧被束缚在一个槽中,则所得绕组被称为集中绕组,并且诱导的总EMF等于诱导的EMF的算术和在一个相1个相位的所有线圈中引起的EMF的算术和极。
但在实际应用中,为了获得平滑的正弦电压波形,交流发电机的衔接绕组不集中,但在不同的槽中分布,以在每个极下形成极性群体。在分布式绕组中,每相线圈侧通过等于相邻槽的角位移的角度彼此移位。因此,每个线圈侧的感应EMF不是等于槽的角位移的角度。
因此,绕组的合电动势是每线圈边感应电动势的相量和。由于它是相量和,必须小于这些感生电磁场的算术和。
如果线圈是集中的,结果电动势将是一个算术和。
根据定义,分布系数是分布绕组相对于集中绕组的合电动势的量度。
我们将其表示为分布在一个极点下某些槽内的所有线圈中感应电磁场的相量和与感应电磁场的算术和之比。分布的因素是,
作为音高因子,分布因子也总是小于单位。
设每个极点的槽数是n。
每极每相位的槽数是m。
每个线圈侧诱导EMF是Ec.
槽之间的角位移,
让我们用交流、直流、DE、EF等表示在一个极点下同一相不同线圈中所产生的电动势。它们的大小是相等的,但它们之间的角是β。
如果我们在AC,CD,DE,EF的BISECTORS上绘制Bisectors。他们会在共同点遇见O.
EMF在每个线圈侧引起,
由于每极每相槽为m,则每极每相每线圈侧所有感应电动势的总算术和,
合起来的电动势是AB,如图所示,
因此,合成电动势
Mβ也被称为电度的相扩散。
分布因子Kd由方程给出的是电动势的基本分量。
如果助势分布包含空间谐波的插槽角间距β基本尺度,将成为r的rβth谐波分量,因此r的分布因子th谐波。