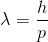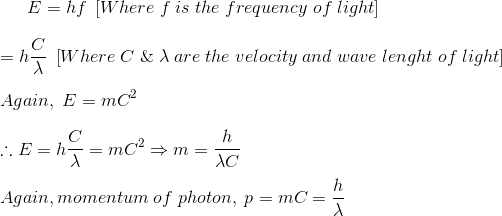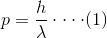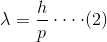随着发展的发展光电效应,克朗佩顿的效果和波尔的原子模型,光明的想法或实际上一般辐射,由粒子或离散组成Quanta.得到了广泛的欢迎。
然而,非常确定的惠更斯原理和杨氏双缝实验的结果清楚地表明,光是波,而不是流粒子。
光通过双缝时所观察到的明显干涉图样,无疑是光的波动性质的结果。这又引起了关于光的本质的争论。1704年,牛顿还通过他的微粒理论提出了光的粒子性质。
这两个理论都没有足够足以解释与光有关的所有现象。因此,科学家开始得出结论,光有波浪和粒子性质。1924年,一位法国物理学家,路易斯德里格利提出了一个理论。He suggested that all particles in this universe is associated with wave nature also, i.e. everything in this world be it a small photon or a giant elephant, everything has an associated wave with itself, it is a different matter that the wave nature is noticeable or not. He assigned a wavelength to each matter with mass m and momentum p as
式中,h为普朗克常数,p = mv, v为物体的速度。
因此,由于大量的大象,它具有非常显着的势头,因此是非常小的波长,我们无法注意到。然而,诸如电子等的小颗粒具有非常小的质量,因此非常明显的波长或波动性。这种De Broglie的理论还有助于我们解释Bohr原子模型中的轨道的离散存在。如果其长度等于其自然波长的整体倍数,则在轨道中存在电子将存在于其自然波长的整体倍数。然后,如果它无法完成其波长,则该轨道将不存在。
Davisson和Germer进一步研究了晶体的电子衍射和用电子轰击双缝后得到的类似干涉图样,加强了德布罗意的物质波理论波粒子二元性理论。
康普顿效应
在光电效应中,光以称为光子的粒子束的形式照射在金属上。一个光子的能量贡献工作功能一个电子的能量同时也为发射的电子提供动能。这些光子是光波的类似粒子的行为。爱因斯坦爵士提出,光是大量被称为光子的能量包的集体效应,每个光子都含有hf的能量。其中h是普朗克常数,f是光的频率。这是光波的一种类似粒子的行为。光波或其他电磁波的类似粒子的行为可以用康普顿效应。
在这个实验中,一束频率为f的x射线O.和波长λO.入射在电子上。通过入射X射线撞击电子之后,发现电子和入射X射线两者相对于入射X射线的轴线散射成两种不同的角度。这种碰撞使能量对话原则就像牛顿粒子的碰撞一样。发现在碰撞之后,电子在特定方向上加速,入射X射线在另一个方向上衍射并且还观察到,衍射射线具有与入射X射线不同的频率和波长。由于光子的能量随频率而变化,可以得出结论,入射X射线在碰撞期间损失能量,并且衍射光线的频率总是小于入射X射线的频率。X射线光子的这种损失能量有助于电子的运动。这种X射线或其光子和电子的碰撞就像是牛顿的颗粒,如广告牌球。
光子的能量由
因此,可以证明光子的动量为
可以写成,
从等式(1)可以得出结论,具有波长λ的电磁波将具有带有动量p的光子。
从等式(2)可以得出结论,具有动量P的粒子与波长λ相关联。这意味着波具有粒子类似的特性,粒子上的粒子也表现出类似的行为。
我们已经说过,这个结论首先是由德布罗意得出的因此这被称为德布罗意假设。运动粒子的波长表示为
式中,p为动量,h为普朗克常数,波长λ为德布罗意波长。德布罗意解释说,当电子围绕原子核运行时,它也会有类似波的行为以及类似粒子的特征。
解密和生态化实验
电子的波形可以以许多不同的方式证明和建立,但大多数流行的实验是1927年年度的分配和生态。在该实验中,它们使用了一束加速电子,通常在镍块的表面上撞击。在镍块上撞击后,观察到散射电子的图案。它们为此目的使用了电子密度监视器。虽然预期电子应在不同角度相对于入射电子束的轴线碰撞后散射,但在实际实验中发现,发现散射电子的密度更特别地比其他角度更大。散射电子的这种角度分布非常类似于光衍射的干涉。因此,这个实验清楚地表明存在波粒子二元性电子。同样的原理也可以应用于质子和中子。