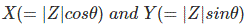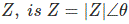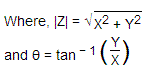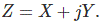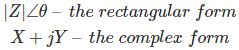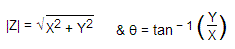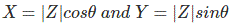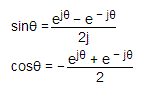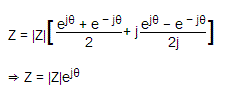矢量代数|矢量图

在学习之前必威电竞赞助重要的是要知道，角的关系主要是电压和当前的在一个系统中。为了了解电压之间的关系，我们应该首先知道向量的定义并经历矢量代数和矢量图。

矢量的定义

存在一些数量的数量，以及它们的作用方向。这种类型的数量称为矢量数量。这就是人们可以制作基本的向量的定义在很少的话。矢量的最基本概念是，这是幅度和方向上的这些数量的表示。每当我们代表任何数量时，它可能有一些行动方向。假设我们说，一个5 n的力，它没有完成图片。
我们应该总是要说方向，即5 n力向上，向下或任何其他方向的力。因此，向量量必须用磁铁矿以及其方向表示。可以通过测量由量和参考轴的方向形成的角度来表示任何量的方向。

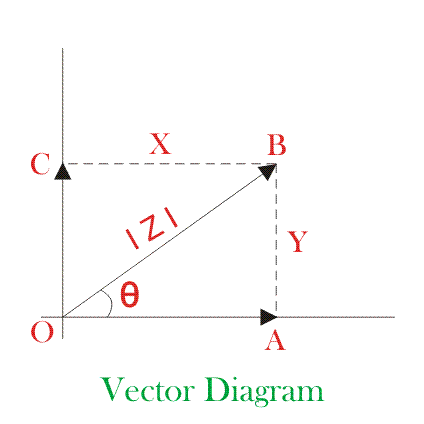
这在这方面矢量图矢量OB具有幅度的z |以参考轴牛角的角度θ。这可以彼此以直角分成两个组件，说出这些是
代表载体的常规方法

矢量代数

现在我们会讨论矢量代数。对于不同的计算，向量必须代数表达。在里面矢量图载体z是矢量图添加其组件x和y的所得到的。
这个矢量可以写入矢量代数作为
其中，j表示组件y垂直于组件x。x轴矢量图被称为“真实”或“阶段”轴，垂直Y轴称为“虚构”或“正交”轴。与正交组件Y相关联的符号'j'可以被认为是逆时针旋转载体的操作员^O.。如果矢量必须逆时针旋转180^O.然后，运算符J必须两次执行其函数，并且由于向量已反转其感觉然后J.j或J.²= - 1

这意味着，j =√

- 1

所以我们已经看到矢量数量可以按照以下不同形式表示，

矩形和复杂形式的矩形的关系

根据此页面上显示的矢量图。载体Z的大小是

从这两个方程式，我们得到，

将这些值X和Y放在复杂的Z形式，我们得到，

上述表达的值称为载体的三通形式。我们再次知道，COSθ和SINθ可以以指数形式表示如下

如果我们在等式z |（cosθ+jsinθ）中将这些上方的呈指数形式的SINθ和COSθ置于我们得到的，

⇒Z = | Z | e^jθ.
这是载体的指数形式。
因此来自上述所有表达式矢量代数和矢量图，可以得出结论，矢量数量可以表示为下面列出的总共四种基本形式