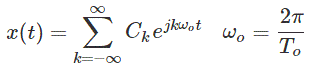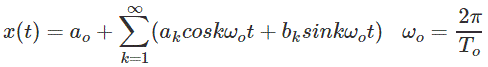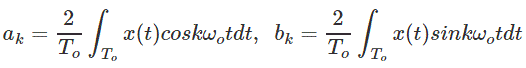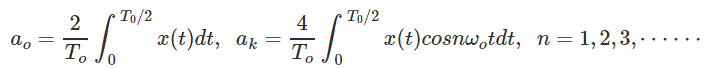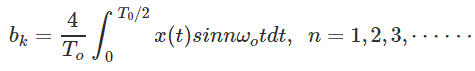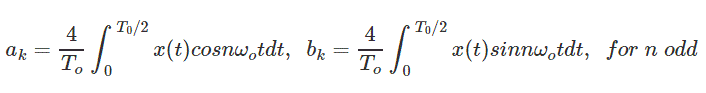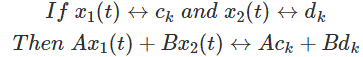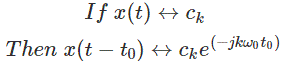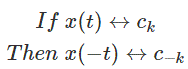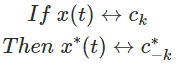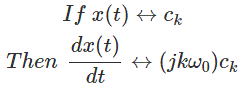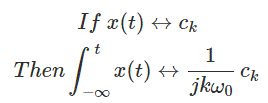三角傅里叶系列

我们已经讨论过了傅里叶系列以指数形式。在本文中，我们将讨论另一种形式的傅立叶系列即。三角傅里叶系列。

三角形式的傅里叶系列表示

傅里叶系列三角形可以容易地从其指数形式衍生。具有基本时段T的复杂指数傅里叶串联表示周期性信号x（t）_O.是（谁）给的

由于正弦和余弦可以以指数形式表示。因此，通过操纵指数傅里叶系列，我们可以获得其三角形式。

这三角傅里叶系列表示具有基本时段T的周期性信号x（t）的表示

哪里A._K.和B._K.是傅立叶系数给出

一种_0.是信号的直流分量，并给出

傅立叶系列的性质

1.如果x（t）是偶数函数即x（ - t）= x（t），然后B._K.= 0且

如果x（t）是偶数函数即x（ - t）= - x（t），然后一种_0.= 0，a_K.= 0且

3.如果x（t）是半对称函数即x（t）= -x（t±t_0./ 2），然后一种_0.= 0，a_K.= B._K.= 0对于k偶数，

4.线性

时间转移

6.逆转时间

7.乘法

8.缀合

9.差异化

10.整合

11.定期卷积

三角形式指数形式与系数之间的关系

当x（t）是真实的，然后a和b，是真实的，我们有

信号的换档轴线的影响

• 在相对于参考时间轴T = 0向左向右移动波形，仅频谱变化的相位值，但幅度频谱保持不变。
• 在向上或向下移动波形时，时间轴仅更改功能的DC值。