一个电网树是分支的集合,它是包含网络中所有节点但不构成任何闭合路径的分支的集合。它类似于网络拓扑结构是一个通信网络。
让我们解释一下电网树如上定义。
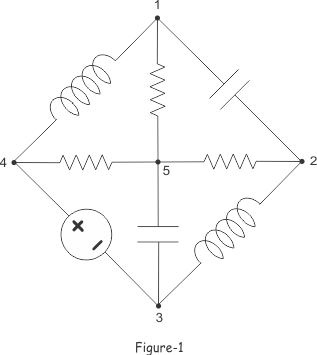
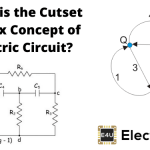
上面的图-1显示了一个包含节点1、2、3、4和5的电网。
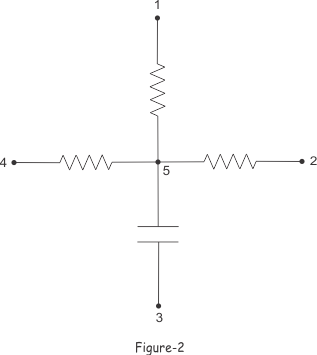
现在,如果我们从电路中去除1-2、2-3、3-4和4-1支路,我们将得到如下图-2所示的图。
上图如图-2所示,包含了网络的所有5个节点,但没有来自任何闭合路径。这是一个电网树.
通过这种方式,这种树的数量可以形成在一个单一电路,它包含相同的5个节点,但不包含任何闭环。
树的树枝也被称为细枝。
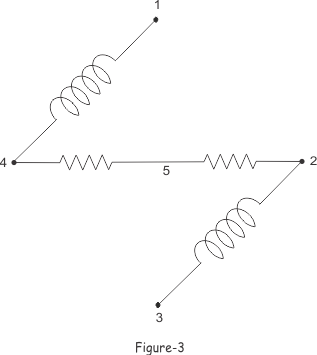
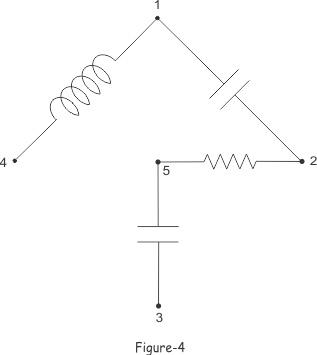
在图2、图3、图4中我们可以看到,该电网络的每棵树都有4个小枝或树枝。网络中的节点数为5。
在这种情况下,
这是一个适用于任何电力网的所有树的通式。一般方程通常写成,
式中,l为一棵树的分支数,n为构成树的网络中的节点数。
电力网络Cotrees
当,由一个电网络形成一个图时,选取一些有选择性的分支。不是树状结构的网络分支被称为链或弦。由这些连杆或和弦构成的曲线图称为余弦图。Cotree可以根据链接关闭或打开。
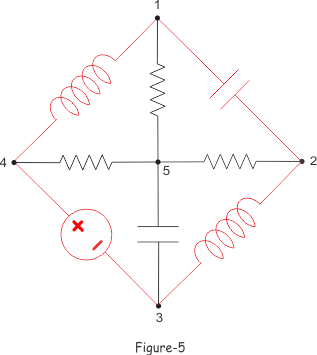
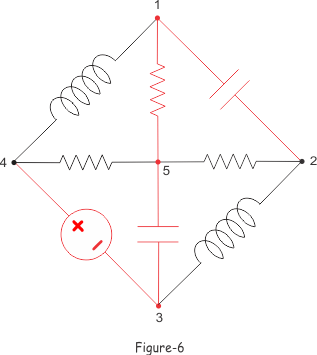
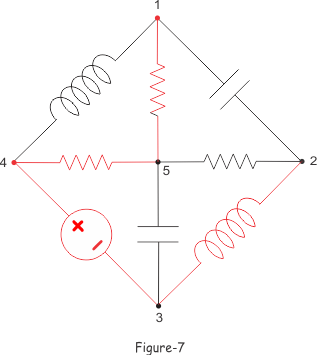
余树在上图中用红色表示。由图-5、图-6、图-7可知,树的分支数与其余树数之和即为电网的总分支数。
所以,如果一个余树的连杆数是l ',那么
式中,l为树中的枝数,b为网络中的枝数。所以,
式中,n为电网的节点数。
电网络树的性质
- 一棵树由电网的所有节点组成。
- 一棵树的分支数小于电网节点数的1。
- 一棵树的任何部分都不能有封闭的路径。
- 在同一个电网中可能有许多不同的可能树。
- 一棵树的分支数与其余树的分支数之和等于其电网络的分支总数。
- 独立的数量基尔霍夫电压定律当一个电网络的余弦或环数等于它的余弦数时,可以形成方程。
- 独立的数量基尔霍夫电流定律当电力网的细枝数等于电力网的细枝数时,可以得到电力网的方程式