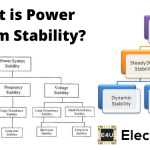
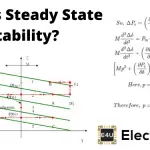
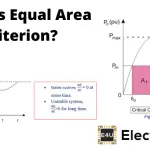
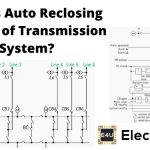
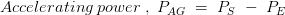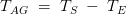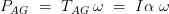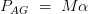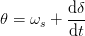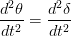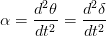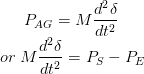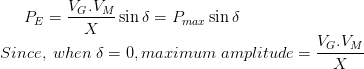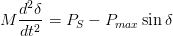同步电力系统返回稳定条件的能力并在从电路元件开启和关闭的非常大的情况下实现的相对大的干扰后保持其同步，或者将故障排放等的清除等电力系统的瞬态稳定性．通常情况下发电系统受到这种故障的影响，因此对于电力工程师来说非常重要，以便在系统的稳定条件下良好。
在一般的实践中，与电力系统中的瞬态稳定性相关的研究是在等于一个摆动所需的最小时段的最小时段中完成，这近似于大约1秒甚至更少。如果在第一次摆动期间发现系统稳定，则假设干扰将减少在随后的摇摆中，并且在这种情况下，系统将稳定。现在要在数学上确定系统是否稳定，我们需要导出挥杆方程电源系统．
用于确定瞬态稳定性的摆动方程
为了确定电力系统的瞬态稳定性摇摆方程，让我们考虑一个同步发电机提供输入轴电源P.S.产生机械扭矩等于tS.如下图所示。这使得机器以ωad/ sec的速度旋转，并且在接收端上产生的输出电磁扭矩和功率表示为tE.和P.E.分别。
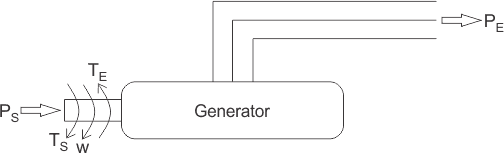
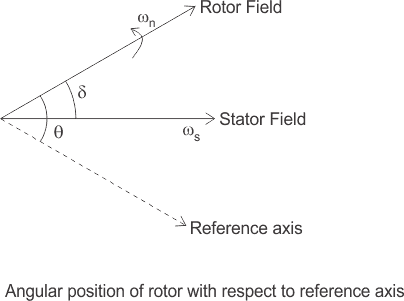
当时，同步发电机用一端供给电源，并且施加到另一端的恒定负载，转子轴和定子之间存在一些相对的角位移磁场，称为负载角δ，其与机器的负载直接成比例。此实例的机器被认为是在稳定状态下运行。
现在，如果我们突然从机器中添加或移除负载，转子相对于定子磁场相应地减速或加速。现在机器的操作条件变得不稳定，转子现在被称为摆动W.R.T定子场和等式，我们获得了载荷角δw.r.t的相对运动。定子磁场被称为摇摆方程用于电力系统的瞬态稳定性。
在这里，为了理解，我们考虑了同步发电机突然用增加量的电磁负荷施加的情况，这导致通过制作p不稳定E.小于p.S.随着转子经历减速。现在给出将机器带回稳定条件所需的加速功率的增加量，
类似地，加速扭矩由，
现在我们知道
（因为t =当前的×角加速度)
此外，角动量，m =iω
但由于加载角位移θ随着时间的推移而连续变化，如下图所示，我们可以写入。
双重区分上面的等式w.r.t时间，我们得到，
有角度的加权
因此，我们可以写，
现在传输的电磁功率由，
因此，我们可以写，
这就是所谓的摇摆方程电力系统的瞬态稳定性．
