当一个电压突然互相应用于电容器,预先没有收到的,电子从源转移到电容器以立即启动。换句话说,电容器中的变化的累积立即开始。由于电荷在电容器中的电荷增加,电容器上产生的电压增加。在电容器上产生的电压来供电电压电压率电容器中的电荷累积相应地减小。当这两个电压变得等于彼此相等时,从源到电容器将没有更多的电荷流。从源到电容和电容到源的电子流量只是电流。
在开始时,此电流将是最大,在特定时间之后,电流将变为零。电容器电流变化的持续时间称为瞬态周期。电容器中的充电电流或其他电量的现象称为瞬态。
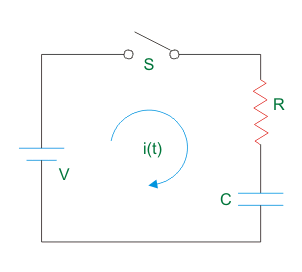
理解电容器的瞬态行为让我们绘制RC电路,如下所示,
现在,如果开关S突然关闭,则电流开始流过电路。让我们当前的在任何瞬间是我(t)。
还要考虑所开发的电压电容器那个即时是vC(t)。
因此,通过申请Kirchhoff的电压法在那个电路中,我们得到了,
现在,如果在此期间(t)期间的电荷转移是q库仑,那么我(t)可以写成
所以,
将I(t)的表达在等式(i)中,我们得到了,
现在相对于我们得到的时间整合双方,
其中,k是恒定可以从初始条件确定。
让我们在接通电路的瞬间考虑瞬间T = 0,从而在上面的等式中,我们得到的,
不会产生电压电容器在t = 0时,它以前没有改变。
所以,
现在,如果我们在上方的方程处放置RC = T,我们得到了
这个rc或产品反抗和电容RC系列电路称为电路的时间常数。因此,RC电路的时间常数是电容器上产生或掉落的电压的时间是电源电压的63.2%。该时间常数的定义仅在电容器最初不变时保持良好。
同样,在接通电路的瞬间I.T = 0时,电容器上不会产生电压。这也可以从等式(ii)中证明。
所以通过电路初始电流是,v / r,让我们认为是我的0.。
现在在任何瞬间,当前的通过电路将是,
现在,T = Rc电路电流。
所以在瞬间,当前通过电容器是初始电流的36.7%,也称为RC电路的时间常数。
时间常数通常表示为τ(taw)。因此,
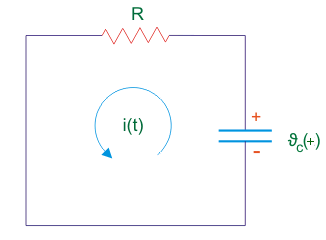
在放电电容器期间瞬态
现在,假设电容器完全充电,即电容器处的电压等于源极电压。现在,如果是电压源断开连接,而是两个终端电池短路循环,电容器将凝视放电装置,通过短路路径均衡两个板之间的电子的不等分布。在两个板中等于电子浓度的过程将继续,直到电容器处的电压变为零。该过程称为电容器的放电。现在我们会检查电容器的瞬态行为在卸货期间。
现在,通过申请从上述电路Kirchhoff当前法律我们得到,
整合双方我们得到,
k是可以从初始值确定的常数。现在,在短路电容器时,
现在,从等式(III),通过应用T =τ= RC我们得到,
同样,当时的电路电流i。τ= rc,
因此,电容器的时间常数,都是电容器电压,θ.C和当前的我占初始价值的36.8%。