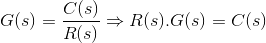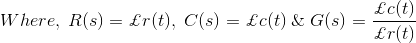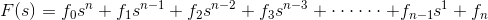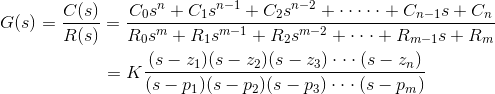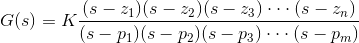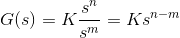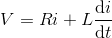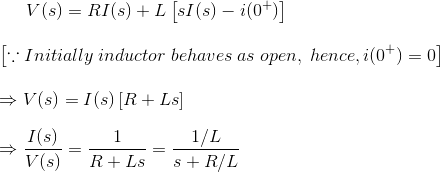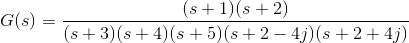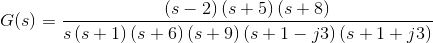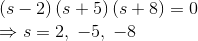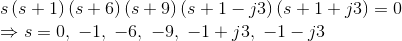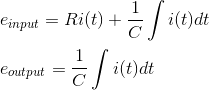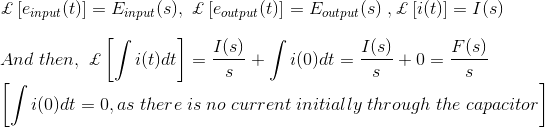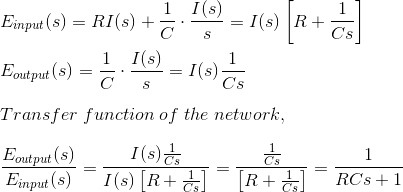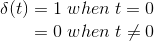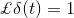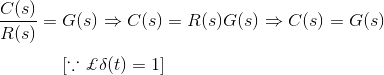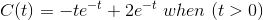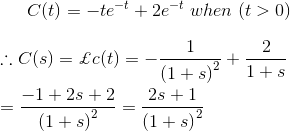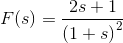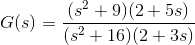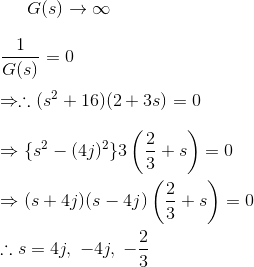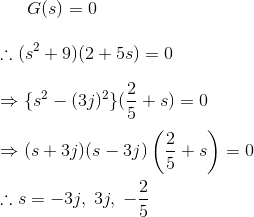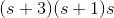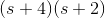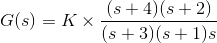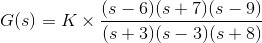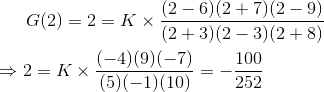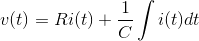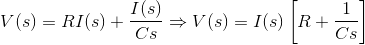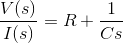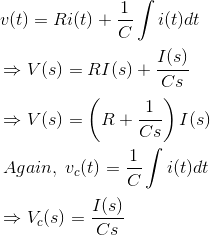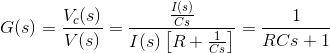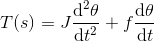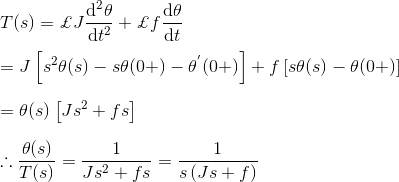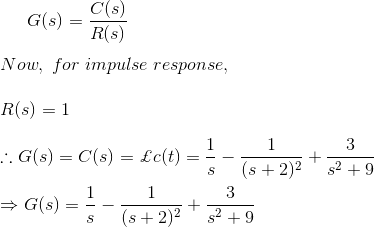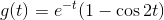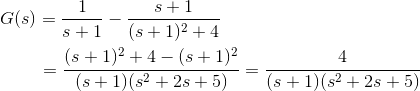控制系统传递函数

一种转换功能表示a的输出信号之间的关系控制系统对于所有可能的输入值，输入信号。框图是一个可视化的控制系统，它使用块表示传递函数，箭头表示各种输入和输出信号。

对于任何控制系统，都存在一个被称为激励或原因的参考输入，它通过传递操作(即传递函数)产生一个导致被控制输出或响应的效果。

因此，输出和输入之间的因果关系是通过a来相互联系的转换功能。

在一个拉普拉斯变换，如果输入用R(s)表示，输出用C(s)表示，则传递函数为:

也就是说，系统的传递函数乘以输入函数得到系统的输出函数。

什么是转移函数

控制系统的传递函数被定义为输出变量的拉普拉斯变换与假设所有初始条件为零的输入变量的拉普拉斯变换的比率。

用于确定控制系统的传递函数的过程如下：

1. 我们形成系统的等式。
2. 现在我们对系统方程做拉普拉斯变换，假设初始条件为零。
3. 指定系统输出和输入。
4. 最后，我们采用输出的拉普拉斯变换和输入的拉普拉斯变换的比率，这是所需的传递函数。

控制系统的输出和输入不一定是同一类的。例如,在必威电子竞技大赛电动马达输入是电信号，而输出是机械信号，因为旋转电机需要电能。类似地，在发电机中，输入是机械信号，输出是电信号，因为发电机需要机械能来发电。

但是对于数学分析，对于一个系统所有的信号都应该用相似的形式表示。这是通过把各种信号变换成它们的拉普拉斯形式来实现的。同时，将系统的输出拉普拉斯传递函数除以输入拉普拉斯传递函数，用拉普拉斯形式表示系统的传递函数。因此，控制系统的基本框图可以表示为


其中r(t)和c(t)分别为输入和输出信号的时域函数。

获得传递函数的方法

得到控制系统的传递函数主要有两种方法。的方法是:

• 框图方法：对于一个复杂的控制系统，推导一个完整的传递函数是不方便的。因此，控制系统中每个元件的传递函数用方框图表示。应用方框图简化技术来获得所需的传递函数。
• 信号流程图：框图的修改形式是信号流图。框图给出了控制系统的图形表示。信号流程图还缩短了控制系统的表示。

转移函数的极点和零

一般来说，一个函数可以表示为多项式形式。例如,

现在类似地，控制系统的传递函数也可以表示为

其中K为传递函数的增益因子。

在上面的函数中，如果s = z₁，或s = z₂，或s = z_3.,……s = z_N，传递函数的值变为零。这些Z.₁, z₂, z_3.z,……_N，是分子多项式的根。至于这些根部分子多项式，传递函数变为零，这些根部称为转移函数的零。

现在，如果s = p₁，或s = p₂，或s = p_3.,……s = p_m，传递函数的值变为无限。因此，分母的根部称为该功能的极点。

现在我们把传递函数写成多项式形式。

现在，让我们考虑对无穷大的方法，因为根部是所有有限数量，与无限的S相比，它们可以忽略它们。所以

因此，当s→∞和n > m时，函数也会有无穷大的值，这意味着传递函数在无穷大s处有极点，并且极点的多重度或阶数为n - m。
同样，当s→∞且n < m时，传递函数的值为零，这意味着传递函数在无穷大的s处为零，且这些零的多重度或阶数为m - n。

转移功能的概念

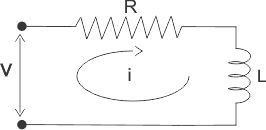
传递函数通常在拉普拉斯变换中表示，只不过是系统的输入和输出之间的关系。让我们考虑一个系统由连接的系列组成电阻（r）和电感在一个(L)电压源（v）。

在这个电路中，电流“i”是由于应用的响应电压(V)的原因。因此电压和当前的电路的可以分别看作是系统的输入和输出。

从赛道上，我们得到，

现在应用拉普拉斯变换，我们得到，

系统的传递函数，g（s）= i（s）/ v（s），输出与输入的比率。
1）让我们通过一个例子解释杆的概念和转移函数的零。

解决方案
该功能的零是-1，-2，函数的极点是-3，-4，-5，-2 + 4j，-2 - 4j。

这里n = 2和m = 5，如n
2）让我们参加控制系统的传递函数的另一个例子

解决方案
在上述传递函数中，如果分子的值为零，则

这些是函数零点的位置。
同样，在上述传递函数中，如果分母的值为零，则

这些是该功能的极点的位置。

随着零的数量应该等于极数，剩余的三个零位位于S→∞处。

网络的传递函数示例

3）

解决方案
在上述网络中，可以明显看出

让我们假设,

考虑到初始条件为零，获取上述方程的拉普拉斯变换，我们得到，

脉冲信号的影响

单位脉冲信号被定义为


单位脉冲函数的拉普拉斯变换为1。

现在，如果输入信号是单位脉冲信号，那么

输出函数与其传输函数相同。

传递函数的例子

1)系统的脉冲响应为

系统的转移功能是什么？
解决方案
对于脉冲响应，系统的输出C（S）等于系统的传输功能。

因此，系统的传递函数为

2)求函数的极点和零点

解决方案

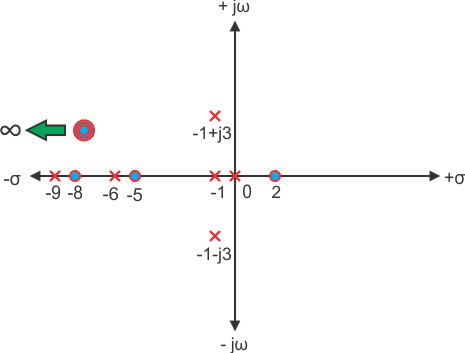
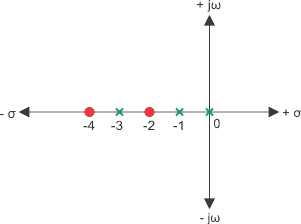
3)极点和零在平面上绘制如下图所示

找到传递函数。
解决方案
这里，极点是S = - 3， - 1,0。
因此，该功能的分母是，

0是-4 - 2。

因此，该功能的分子将是，

因此，传递函数为，

其中，K是增益因子控制系统。
4)在s = 2时，求一个值为2的传递函数的增益因子K，传递函数为

解决方案
现在，根据问题的条件，

5)求下列网络的传递函数。

解决方案
从我们得到的电路来看，

现在申请拉普拉斯变换在双方我们得到，

作为所应用的电压是原因和相应的充电当前的是效应，所施加的电压可视为输入，充电电流可视为输出。

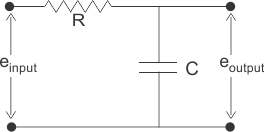
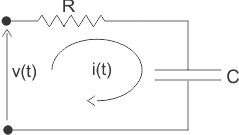
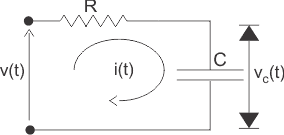
6）找到下面给出的网络的传递函数，

解决方案
在上图中，施加电压V（t），输出被测量，因为电压出现在横跨电压电容器c是v_C(t)。

拉普拉斯变换传递函数的

7）由于施加扭矩T抵抗轴承摩擦F，旋转内轴J的轴旋转成角θ。找到系统的传递函数。
解决方案
上述声明的微分方程形式是

对系统的两边做拉普拉斯变换，

由于所施加的力矩是输入的，而输出的角位移是系统的输出。
8）系统的脉冲响应由c（t）= 1 - te给出^{2 t}+ sin3t。求系统的传递函数
解决方案

9）找到由提供系统的脉冲响应的传递函数

解决方案