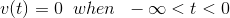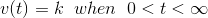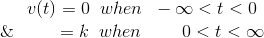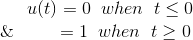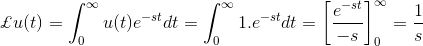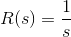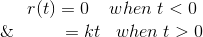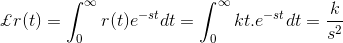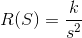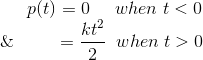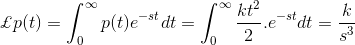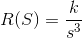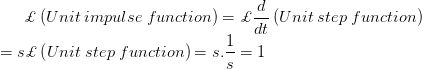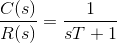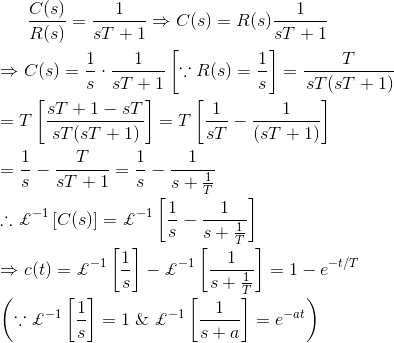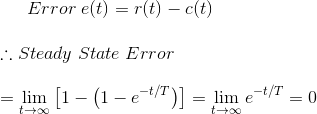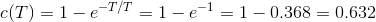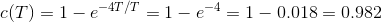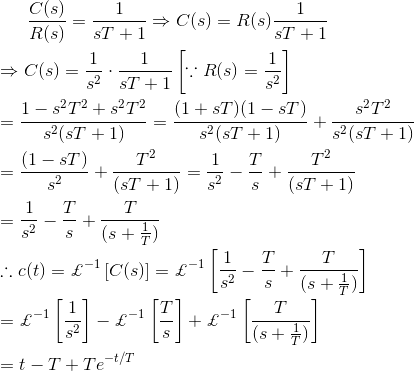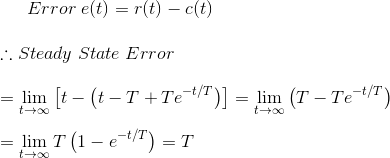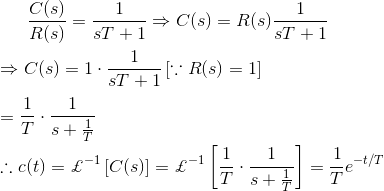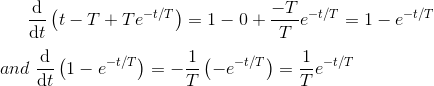在一个控制系统,可能有一些能量存储元件附着在它。储能元件一般是电感器和电容器在电气系统的情况下。由于存在这些能量存储元件,如果系统的能量状态被扰乱,则需要一定时间的时间来从一个能量状态变为另一个能量。系统所采取的确切时间将一个能量状态改为另一个能量状态被称为瞬态时间和价值和模式电压和潮流这段时间称为暂态响应。
瞬态响应通常与振荡相关联,这可能在自然界中持续或腐蚀。系统的确切性质取决于系统的参数。任何系统都可以用线性微分方程表示。该线性微分方程的解决方案给出了系统的响应。通过时间和解决方案的线性微分方程表示控制系统的表示及其解决方案控制系统的时域分析。
阶跃函数
让我们以一个独立的电压源或者电池跨越的电压表通过开关,s。从下图清楚,只要开关S打开时,电压表终端之间的电压就会为零。如果电压表终端之间的电压表示为V(t),则可以在数学上表示情况
现在让我们考虑在T = 0时,开关关闭,立即电池电压V伏特出现在电压表上,这种情况可以表示为,
结合上述两个方程我们得到
在上述方程中,用1代替V,得到单位阶跃函数,定义为
现在让我们来研究拉普拉斯变换单位阶段功能。通过将此功能乘以e可以获得任何功能的拉普拉斯变换-英石并集成到0到无限远。
图6.2.1
如果输入是R(s),则
斜坡函数
由与原点相交的倾斜直线表示的功能称为斜坡函数。这意味着此函数从零开始,随时间线性增加或线性增加。斜坡函数可以表示为,
在上面的方程中,k是直线的斜率。
无花果6.2.2
现在让我们来研究拉普拉斯变换斜坡函数。正如我们介绍任何功能的Laplace变换,就可以通过将此功能乘以e来获得-英石并集成到0到无限远。
抛物线函数
这里,当时间t <0时,函数的值是零,并且在时间t> 0时是二次的。抛物线函数可以定义为,
现在让我们检查抛物线功能的拉普拉斯变换。正如我们介绍任何功能的Laplace变换,就可以通过将此功能乘以e来获得-英石并集成到0到无限远。
图6.2.3
脉冲函数
当输入在无穷小的持续时间内突然应用于系统时,就会产生脉冲信号。该信号的波形用脉冲函数表示。如果这个函数的大小是一个单位,那么这个函数称为单位脉冲函数。阶跃函数的一阶导数是脉冲函数。因此,单位脉冲函数的拉普拉斯变换就是单位阶跃函数一阶导数的拉普拉斯变换。
图6.2.4
一阶控制系统的时间响应
当传输函数的分母中S中的S的最大功率是一个时,传递函数表示第一阶控制系统。通常,第一阶控制系统可以表示为
阶跃函数的时间响应
现在给系统一个单位阶跃输入,然后我们分析输出的表达式:
图6.3.2从误差方程可以看出,当时间接近无穷时,输出信号以指数形式达到一个单位的稳态值。当输出以指数方式接近输入时,当时间接近无穷时,稳态误差为零。
让我们在输出方程中放入T = T,然后我们得到,
该T被定义为响应的时间常数和响应信号的时间常数是该信号达到其最终值的63.2%的时间。现在,如果我们在上述输出响应方程中放入T = 4T,那么我们得到,
当响应的实际值达到所需值的98%时,据说信号达到其稳态条件。这种所需时间来达到信号的98%的所需值被称为设定时间,自然设定时间是响应的时间常数的四倍。在设定时间之前的响应条件称为瞬态条件和设置在设置时间后响应的条件被称为稳态条件。从这个解释中,很明显,如果系统的时间常数较小,系统的响应越快达到其稳态条件。
斜坡函数的时间响应
在这种情况下,在稳态条件下,输出信号滞后于输入信号的时间等于系统的时间常数。系统的时间常数越小,响应的位置误差越小。
脉冲函数的时间响应
在上述控制系统的时间响应的解释中,我们已经看到步函数是斜坡函数的第一导数,并且脉冲函数是步进函数的第一导数。还发现步进功能的时间响应是斜坡函数的时间响应的第一个导数,并且脉冲函数的时间响应是步函数的时间响应的第一导数。