等效电压和电阻:它是什么?(达维宁定理betway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是达维宁定理(达维宁等价)?

Thevenin定理(又称Helmholtz-Thévenin定理)指出任何线性电路只包含电压源、电流源和抵制可以用电压源的等效组合代替（V_TH.)与单个电阻(R_TH.）连接在负载上。该简化电路称为临时等效电路。

戴维宁定理是由一位法国工程师发明的Léon Charles Thévenin(因此得名)。

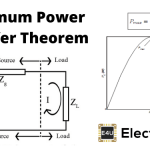
用达维宁定理将一个复杂的电路转换成一个简单的双端达维宁等效电路。一个等效电路包含一个Thevenin电阻和Thevenin电压电源与负载相连，如下图所示。

抗性（r_TH.）也称为等效电阻。和母线电压（v_TH.)是一个开路电压在负载终端。

本定理仅适用于线性电路。如果电路有元素，如半导体元件或气体放电组件，则无法申请紫色的定理

戴维南等效公式

如图1(b)所示，Thevenin等效电路包含等效电压源、等效电阻和负载。

戴文宁等效电路为单回路。如果我们对这个回路施加KVL(基尔霍夫电压定律)，我们可以找到通过负载的电流。

根据KVL，

$\ [v_ {th} = i（r_ {th} + r_l）\]$

$I = \frac{V_{th}}{(R_{th} + R_L)}$

如何找到Thevenin等效电路

临时等效电路包含近距离电阻和临时电压源。因此，我们必须为临时等效电路找到这两个值。

戴维南等效电阻

为了计算Thevenin等效电阻，请去掉原电路中的所有电源。电压源短路当前的打开来源。

因此，剩下的电路只有电阻。现在，计算总阻力之间的开路连接点跨负载终端。

通过制造串联和平行连接来计算等效电阻。并找到等效电阻的值。这种电阻也称为易源性（r_TH.)．

戴维南等效电压

为了计算临时等效电压，负载阻抗是开放式的。并在负载端子上找到开路电压。

等效电压（v_eq.）等于通过两个负载端子测量的开路电压。理想电压源的该值用于临时等效电路。

等效相关源

如果一个电路网络包含一些相关的源，则用另一种方法计算Thevenin电阻。在这种情况下，依赖源保持原样。你不能移除(断开或短路)电压或电流源。

在依赖源的情况下，有两种方法可以找到母性阻力。

方法1

在这种方法中，我们必须求出达维宁电压(V_TH.）和短路电流（i_SC.)．将这些值代入下式，求出Thevenin电阻。

$R_{th} = \frac{V_{th}}{I_{sc}}$

临时电压与端子A和B上的电压相同。并且我们具有临时电压的值。通过短路负载端子获得短路电流并找到通过短路分支的电流。

在计算短路电流时，电压和电流源保持原样。不要打开或短路电源，无论它是依赖或独立的电源。

方法2

在这种方法中，电压源的一个额外已知值(V₁)通过负载端子连接。求电流(I₁通过保持所有相关和独立的来源来通过电压源。

获取这些值后，将它们放入以下等式中以找到母性阻力。

$\ [r_ {th} = \ frac {v_1} {i_1} \]$

等效电路例子

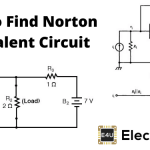
示例1 - 找到通过电阻器r的电流₁

步骤1删除R._L.= 4Ω分支。

步骤2找到Thevenin等效电压(V_TH.)．

外环应用KVL;

$12 = r_1 i_1 + r_2 i_2$

（1） $\begin{equation*} 12 = 4I_1 + 4I_2 \end{equation*}$

从电流来源，我们可以找到第二个等式。

（2） $\ begin {arearation *} i_2 - i_1 = 3 \] \ end {公式*}$

通过求解方程-1和2，可以求出电流I的值₁和我₂．

$i_2 = 5a$

电阻R上的电压₂=4Ω与A与B之间的电压相同。它与等效电压是相同的。

因此,

$\ [v_ {ab} = v_ {th} = i_2 \ times r_2 \]$

$V_{th} = 5 \times 4$

$\ [v_ {th} = 20v \]$

步骤3找到母线等效电阻（r_TH.)．

为了找到Thevenin等效电阻，我们必须去掉所有电压源(因为所有电源都是独立的电源)。拆除电源;电压源为开路，电流源为短路。

这里，两个电阻都并联。因此，临时的等效电阻是;

$R_{th} = 4 || 4$

$\ [r_ {th} = 2 \ omega \]$

步骤4用V的值完成一个等效电路_TH.和R_TH.．

将KVL应用于上述电路;

$20 = 2i + 4i$

$\ [20 = 6i \]$

$\ [i = \ frac {20} {6} \]$

$I = 3.33a$

因此，通过负载的电流为3.333A。

示例2-找到通过电阻器的电流₁

步骤1删除分支R₁= 4Ω。

步骤2计算Thevenin等效电压(V_TH.)．

如果考虑外部循环，它将如下图所示。

电流通过电阻器r₂=2Ω是3a。因此，电压越过电阻器r₂是;

$V_B = V_{R2} = 2 \times 3 = 6v$

我们已经开放了具有电阻器r的分支₁．所以电流I_一种等于0。独立源的电压为零。因此，在计算V时可以忽略它_TH.．

端子A与16V电压源连接。

$v_a = 16v$

端子B与电阻器R连接₂．电阻跨越电阻为6V。

因此，点A和B之间的潜在差异是;

$v_ {ab} = v_a - v_b$

$\ [v_ {ab} = 16 - 6 \]$

$v_ {ab} = 10v$

此电压与戴文宁等效电压相同。因此,

$\ [v_ {th} = v_ {ab} = 10v \]$

步骤3计算Thevenin等效电阻(R_TH.)．

由于给定电路有一个相关的源，我们不能直接求出R的值_TH.．为此，我们将使用上述提示方法。在这里，我们将使用方法-1。

在这种方法中，我们保留所有受抚养人和独立的来源。并找到紫色等同电压的值（v_TH.)和短路电流(I_SC.)．

我们已经拥有v的价值_TH.．因此，我们需要计算I的值_SC.通过短路A和B.

在外环应用KVL;

$16 - 4 i_a = 2 i_2$

$i_a = i_1$

$16 - 4i_1 = 2i_2$

（3） $\ begin {arearation *} 4i_1 + 2i_2 = 16 \ end {等式*}$

我们可以从电流源找到第二个等式。它是;

（4） $\begin{等式*}I_2 - I_1 = 3 \end{等式*}$

通过求解方程-3和4;我们可以求出电流I的值₁和我₂．和现在的我₁是我们需要的电流(我_SC.)．

$I_1 = I_{SC} =\frac{5}{3} A$

现在，将这些值放在以下等式中;

$R_{th} = \frac{V_{th}}{I_{SC}}$

$\ [r_ {th} = 6 \ omega \]$

步骤4戴维南等效电路。

现在，写下V的值_TH.和R_TH.在Thevenin等效电路中。

将KVL应用于循环;

$10 = 6i + 4i$

$\ [10 = 10i \]$

$I = 1a$

Thevenin和Norton等效电路

theven's和诺顿的定理用于电路分析，将复杂网络转化为简单网络。在戴维宁定理中，一个复杂的电路转换成一个戴维宁等效电路。同样地，在诺顿定理中，一个复杂的电路可以转换成诺顿等效电路。

诺顿等效电路由一个与负载并联的诺顿等效电阻和诺顿电流源组成。诺顿等效电路如下图所示。

计算方法，Norton等效电阻与紫色等效电阻相同。

$\ [r_ {th} = r_n = r_ {eq} \]$

戴维宁等效电路由一个电压源(戴维宁电压)和诺顿等效电路由一个电流源(诺顿电流)组成。

考虑将网络转换为Thevenin和Norton等效电路。在这两种电路中，如果你发现负载上的电流和电压，它将与原始电路的值相同。

如果我们想找到紫色和诺顿等效电路之间的关系，我们需要找到紫色电压和诺顿电流之间的关系。

这个关系可以通过欧姆定律;

$V_{th} = I_N R_{eq}$

达维宁定理的局限性

在电路分析中，戴维南定理被广泛应用于求解复杂电路。

然而，在Thevenin的定理有一些局限性，下面列出。

本定理不适用于单方面网络。单侧网络意味着网络的操作和行为通过网络的各个组件依赖于电流方向。
戴维宁定理只适用于由线性元素组成的网络。它不能适用于非线性元素。
电路和负载之间不应该有任何磁力耦合。
不应有任何受控源，从电路的一些其他电路部分控制。

Videoin博物馆定理的视频解释

对于那些想要视频解释找到Thevenin等效电路的人，我们在下面提供了一个。