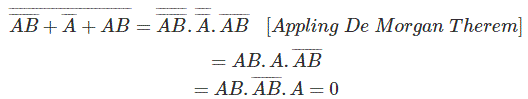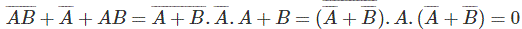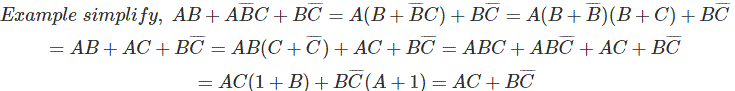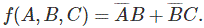布尔代数或转换代数是一种以二进制系统来执行不同数学运算的数学逻辑。这只有两个元素1和0，所有的数学运算都要通过它们来完成。只有三种基二进制运算，AND, OR和NOT，所有简单和复杂的二进制数学运算都可以通过它们来完成。在布尔代数中有许多规则，这些规则是用来进行数学运算的。
在布尔代数，变量用大写字母A, B, C等表示，每个变量的值可以是1或0，没有其他的。
一些基本的逻辑布尔运算
和操作,
或操作,
不操作,
一些基本定律布尔代数，
一个。0 = 0，其中A可以是0或1。
一个。1 = A A可以是0或1。
一个。A = A，其中A可以是0或1。
一个。Ā = 0其中A可以是0或1。
A + 0 = A A可以是0也可以是1。
A + 1 = 1 A可以是0也可以是1。
A + Ā = 1
A + A = A
A + B = B + A A和B可以是0或1。
一个。B = B。A A和B可以是0或1。
的法律布尔代数也适用于两个以上的变量，比如，
布尔代数的累积定律
布尔代数的结合律
布尔代数的分配律
冗余的文字规则
从真值表，
| 输入 | 输出 | ||
| 一个 | B | ĀB | A + BĀ |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
| 输入 | 输出 | |
| 一个 | B | A + B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
从真值表可以证明，
布尔代数的吸收定律
真理表证明，
| 输入 | 输出 | ||
| 一个 | B | AB | A +。B |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
A和A+A。Bcolumn is same.
从证据真值表，
| 一个 | B | A + B | A.X (A + B) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 |
A和A.X或A(A+B)列是相同的。
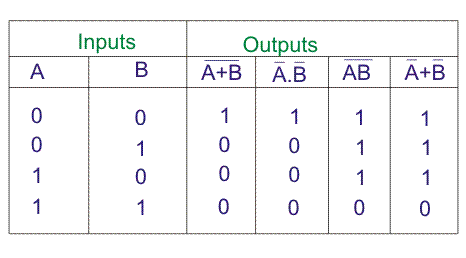
德摩根定理,
从证据真值表，
布尔代数的例子
这是另一种简化复杂布尔表达式的方法。在这个方法中，我们只使用三个简单的步骤。
- 补全整个布尔表达式。
- 将所有or更改为and，并将所有and更改为or。
- 现在，补全每个变量并得到最终表达式。
通过这种方法,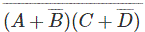
将首先补全，即。
.现在把all(+)改成(.)，把(.)改成(+)。
现在，对每个变量进行补充，
这是布尔表达式的最终简化形式，
它与应用得到的结果完全相等德摩根定理．
另一个例子,
第二种方法,
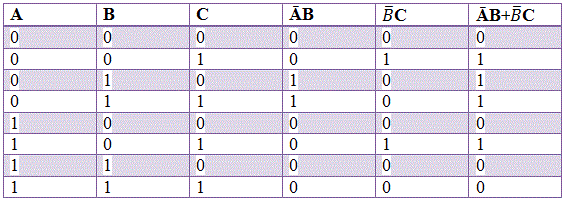
真值表中布尔函数的表示。
让我们考虑一个布尔函数，
现在我们来表示函数真值表．
