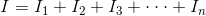叠加定理

让我们理解这个表述。

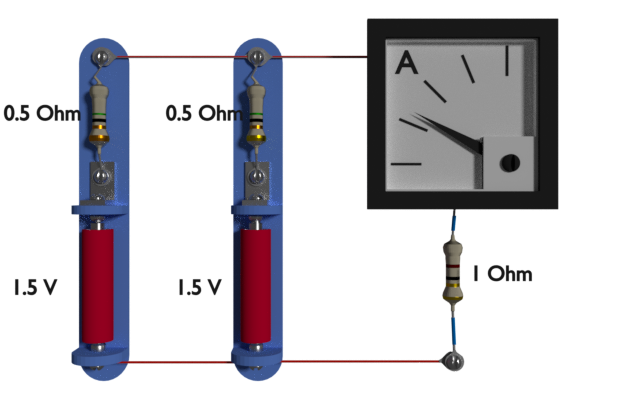
这里，电路中有两个1.5伏的电池。在这种情况下当前的通过1欧姆的抵抗是1.2安培。
的安培表表示上图中的这个值。

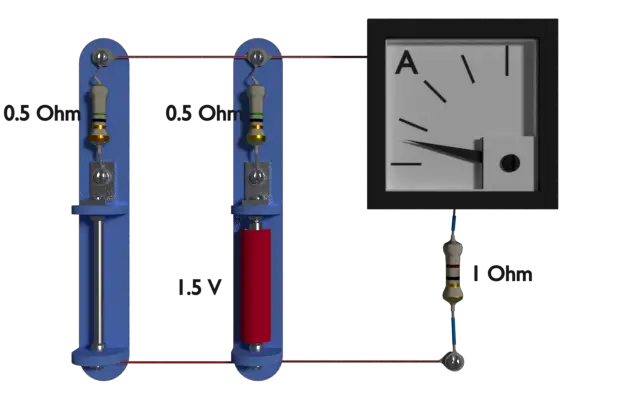
现在，我们替换左边电池由短路所示。在这种情况下，流过1欧姆电阻的电流是0.6安培。电流表显示上图所示的这个值。

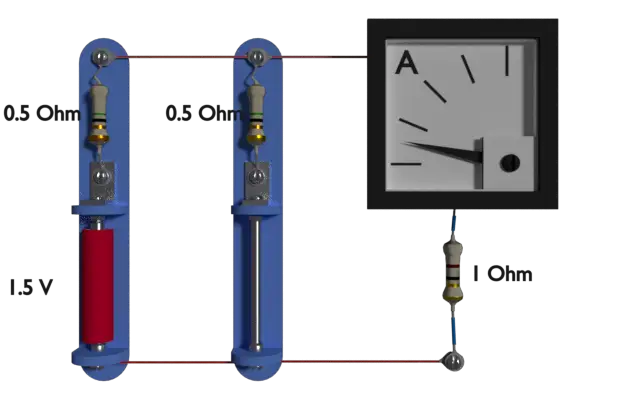
现在，我们用如图所示的短路替换右边的电池。在这种情况下，流过1欧姆电阻的电流也是0.6安培。的安培表如上图所示，表示此值。
1.2 = 0.6 + 0.6
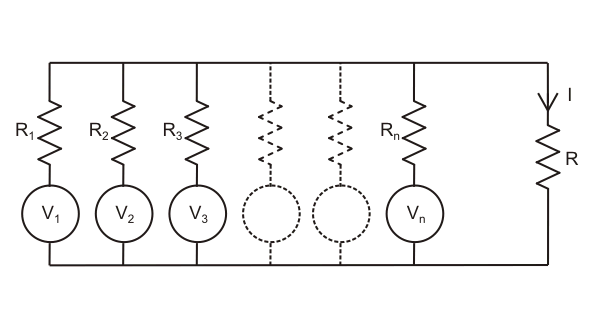
我们可以说，如果我们连接an的一个分支电路用数量电压和电流源全部的当前的通过这个支路的是由每个单独的电压或电流源贡献的所有单独电流的总和。这个简单的概念用数学表示为叠加定理．

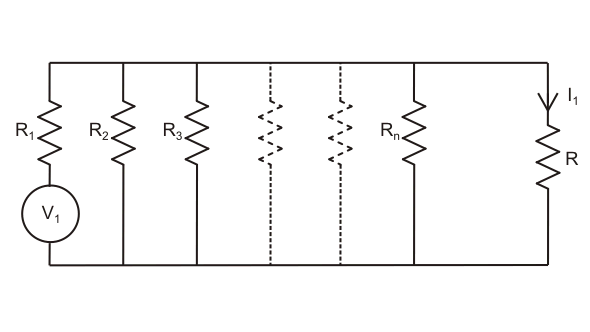
而不是具有如上所示的两个来源，而存在在电路中作用的n个源，因为我电流流过电路的特定分支。

如果有人把电路里的所有电源都换成内部的电阻除了第一个电源，它现在沿着电路作用并提供电流I₁通过该分支，然后他重新连接第二个来源，并取代第一个来源的内部阻力。

现在通过这个分支的电流可以假设为I₂．

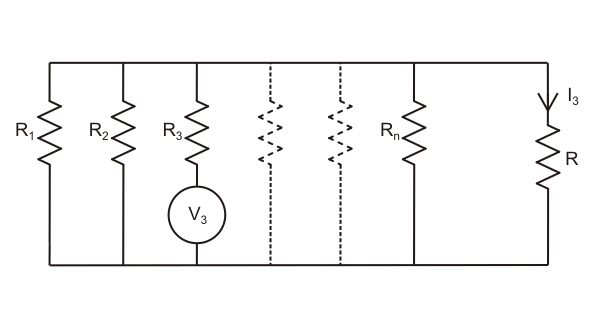
同样地，如果他重新连接第三个电源，用第二个电源的内阻替换它。通过这个分支的电流，单独假设为I_3.．

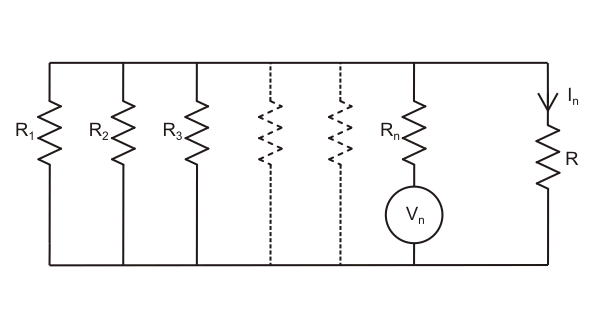
同样,当n^th电源单独作用于电路中，所有其他的电源都被它们的内部电源所取代电抗性我说_n电流流过电路的上述支路。

现在根据叠加定理当所有电源同时作用于电路时，通过支路的电流只不过是这些单独作用于电路的电源所产生的单独电流的总和。

电源可能是两种，其中一个是电压源和其他目前的来源．当我们从电路中取出电压源时，电压贡献到电路变为零。所以要获得零电势差在连接移除的电压源的点之间，这两个点必须短路循环零电阻路径。为了更精确，可以通过其内阻更换电压源。现在，如果我们从电路中删除电流源，则电流由此源贡献将变为零。零电流意味着开路。因此，当我们从电路中删除电流源时，我们只需断开电路终端的源，并保持两个端子打开循环。由于电流源的理想内部电阻无限大，从电路中移除电流源可以替代地称为其内部的电流源电阻．因此，对于叠加定理，用短路代替电压源，用开路代替电源。

这个定理只适用于线性电路，即由电阻组成的电路欧姆定律是有效的。在具有非线性电阻的电路中，如热离子阀、金属整流器，此定理将不适用于。这是一个比其他许多电路定理更费力的定理。但该方法的主要优点是避免了两个或多个联立方程的解。但稍加练习之后，就可以直接从原电路图中写出方程，从而节省了绘制额外电路图的工作量。为了更好地理解程序，我们提供了不同的步骤叠加定理如下所示,

步- 1
用它们的内阻替换除一个以外的所有源。

- 2步
使用简单确定各个分支中的电流欧姆定律．

- 3步
使用每一个来源，轮流作为唯一的来源，重复这一过程。

- 4步
由于每个来源，在特定分支中添加所有电流。这是当同时发挥在电路上的所有源时，该分支处的电流所需值。

叠加定理的例子

假设有两个电压源V₁和V.₂同时作用于电路。
由于这两个电压源，假设电流I流过电阻R。

现在取代V₂短路，保持V₁在它的位置和测量电流电阻，R.说是我₁．
然后替换，v₁通过短路，重新连接V₂测量通过相同电阻R的电流，称其为I₂．
现在如果我们把这两个电流相加₁和我₂我们会得到电流等于流过R的电流，当两个电压源都是V时₁和V.₂同时作用于电路。这是我₁+我₂= I.

视频演示叠加定理的一个例子