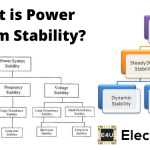
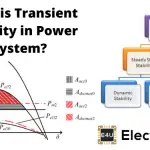
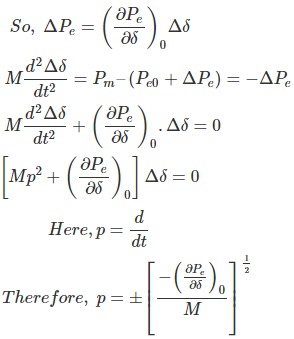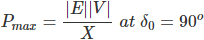作为一种介绍,我们需要了解电力状态稳定性。在经受某些干扰后,系统将返回其稳态状态的能力。我们现在可以考虑一个同步发电机理解这一点电力系统稳定性。发电机与连接到它的其他系统同步。连接到它的总线和发电机将具有相同的相位序列,电压和频率。因此,我们可以说,这里的电力系统稳定性是电力系统恢复其稳定条件的能力,而不会在受到任何干扰时影响同步。该系统稳定性被分为 -瞬态稳定性,动态稳定性和稳态稳定性。
瞬态稳定性:对突发大扰动的电力系统研究。
动态稳定性:对小持续干扰的电力系统研究。
稳态稳定性
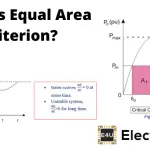
这是一种暗示系统工作状态的小和逐渐变化或变化。目的是在将同步失去同步之前确定机器中的装载更高限制。负载缓慢增加。
可以在不影响同步的情况下传送到系统的接收端的最高功率被称为稳态稳定性极限。
摇摆方程是已知的
P.m→机械电力
P.E.→电力
Δ→负载角
H→惯性常数
ω.S.→同步速度
考虑上述系统(上图),用于在稳态电力传输上运行
假设电力增加了少量说ΔPE.。结果,转子角度变为
从δ.0.。
P→振荡频率。
特征方程用于由于较小的变化而确定系统稳定性。
系统稳定条件
不稳定损失,最大动力传输由
假设系统处于低于稳态稳定性限制的操作时的条件。然后,如果阻尼非常低,则可以连续振荡冗长的时间。持续存在的振荡是对系统安全的危害。| V.T.|应通过调整激发来保持每个负载的常数。这是为了保持稳态稳定性限制。
- 系统永远不能高于其稳态稳定性极限,但它可以超出瞬态稳定性极限。
- 通过减少X(电抗)或通过升高| e |或通过增加| V |,可以提高系统的稳态稳定性极限。
- 两个改善稳定极限的系统是快速激励电压和更高的激励电压。
- 减少x传输线它具有高电荷,我们可以采用平行线。