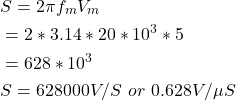回转速率:是多少?公式、单位及测量方法| Electrical4Ubetway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是转换率？

在电子学中，回转速率定义为输出的最大速率电压单位时间的变化。它用字母s表示。旋转速率帮助我们识别振幅和最大输入频率适合A.运算放大器（运算放大器）使输出不会显着扭曲。

转换速率应尽可能高，以确保最大的未置换输出电压摆幅。

压摆率是确保运算放大器可以提供可靠输入的输出的关键因素。压摆率随电压变化而变化获得．因此，它通常以Unity（+1）增益条件指定。

通常通用装置可以具有10的转换速率 $v / \ mu s$ ．这意味着当将大的步进输入信号施加到输入时，电子设备可以在1微秒内提供10伏的输出。

转换速率公式

转换速率的等式由

$\{对齐*}开始S = \压裂{dV_0} {dt} | _m_a_x_i_m_u_m \, \,伏特/ \μS \{对齐*}$

在哪里 $V_0$ 是放大器产生的输出作为时间t的函数。

转换率单位

电子电路的旋转速率定义为单位时间内电压的变化率。转换速率的单位是伏特/秒或 $v / \ mu s$ ．

如何衡量转换率?

旋转速率是通过对输入级施加一个阶跃信号来测量的运放测量在输出信号幅度的10％至90％的输出时发生变化率。通常，施加的步长信号大，其约为1V。

由输出电压波形测量回转率为:

$\ begin {aligne *}转换速率（s）= \ frac {dv_0} {dt} = \ frac {v_0 _（_ 9_0 _ \％_） - v_0 _（_ 1_0 _ \％_）} {t_（_ 9_0 _ \％_） - t_（_1_0 _ \％_）} \结束{align *}$

回转速率可以用一个示波器A.功能发生器．

用于转换速率测量的电路如下图所示。

输入和转换有限输出电压波形如下图所示。

运算放大器的转换率

转换速率决定了OP-AMP快速改变输出的能力，因此它决定了给定OP-AMP的操作的最高频率。

运放的转换速率会限制电路的性能，如果超出了它的限制，它会扭曲输出波形。

由于电路配置，OP-AMPS可能具有不同的转换和负转换的速率。

在理想情况下，旋转速率应是无限的，在实际中应尽可能高。的回转速率IC 741运放只有0。5 $v / \ mu s$ 这是它的主要缺点。因此，它不能用于高频应用。

放大器中的压摆率限制

OP-AMP输入阶段的高增益：

现代运算放大器使用具有跨电传导特性的高增益差分输入阶段。这意味着放大器在输入级处采用差分输入电压，并在输出级产生输出电流。请注意，跨导是转移的电导它是一种电气特性，定义为通过设备输出到输入端的电压的电流。数学上它表示为 $g_m = \ frac {i_o_u_t} {v_i_n}$ ．

该放大器的这种传导电导通常非常高，也在此，产生放大器的大开环增益。这意味着小输入电压可以使输入级饱和。在这种饱和条件下，阶段产生近似恒定的输出当前的作为一个常数目前的来源．在这种情况下，放大器输出端的变化率受到严重限制。这限制了运算放大器的转换速率。

运放第二级频率补偿:

提供稳定、频率所有运放都采用补偿来降低高频响应，这对转摆率有相当大的影响。减少的频率响应限制了发生在放大器输出端的变化率，因此它影响运算放大器的转换速率。

现在，频率补偿在运放的第二级是低通特性，它类似于积分器．因此，恒流输入将产生线性增加的输出。如果第二阶段有有效的输入电容C和电压增益a₂，则回转速率可表示为

${对齐*}\开始转换速度(S) = \压裂{I_c_o_n_s_t_a_n_t}} {C a₂\{对齐*}结束$

我在哪里_不变是第一阶段的恒定电流饱和．

温度：

转换速率是温度依赖性参数。当信号上升时，发生正面转换速率，并且当信号下降时发生负转换速率。通常，放大器的转换速率随着温度的增加而增加。

转换速率与带宽

转换率

压摆率是放大器可以响应输入水平突然变化的最大速率。转换速率可以扭曲（或限制）由OP-AMP放大的任何信号。

输入正弦信号乘以运算放大器的增益，得到的斜率大于运算放大器的转摆率。因此输出的波形将是一条直线而不是一个曲线段正弦．这种效应是非线性的。因此，回转可以改变或扭曲信号的形状。

带宽

放大器的带宽或功率带宽是所有信号频率被几乎相等地放大(没有失真)的频率范围，也就是运放传递函数中的极点所导致的频率范围低通滤波器行为即，信号的幅度随着频率的增加而减小，并且发生相移。这种效果是线性的，它们不会产生输出信号的失真。

运放的带宽应该尽可能大。它应该能够从零频率放大信号。因此，运放的增益在频率从0到无穷之间应该是恒定的。带宽用赫兹表示。

转换速率与全功率带宽的关系

假设输入信号 $V_S$ 是正弦波，我们可以得到放大器产生不失真输出的最大频率值。

（1） $\begin{equation*} V_S = V_m sin\omega t \end{equation*}$

现在，为了统一利益非反相放大器，输出完全等于输入。

$\begin{align*} V_0 = V_m sin\omega t \end{align*}$

对上面的方程两边求导，

$\begin{align*} \frac{dV_0}{dt} = \frac{d}{dt} V_m sin\omega t \end{align*}$

(2） $\ begin {arearation *} \ frac {dv_0} {dt} = \ oomega v_m cos \ oomega t \ end {等式*}$

现在, $\ frac {dv_0} {dt}$ 将在 $Cos = 1 (t=0^0)$ 和最大值 $\ frac {dv_0} {dt}$ 就是回转速率s，代入方程(2)

(3） $\ begin {arequation *} s = \ frac {dv_0} {dt} | _m_a_x_i_m_u_m = \ oomga v_m = 2 \ pi f_m v_m \，\，v / sec \ end {arequation *}$

在那里, $f_m$ = Hz中的最大信号频率

$V_m$ =信号的最大峰值电压

重新排列等式（3）中的术语，我们得到

（4） $\ begin {arearation *} f_m = \ frac {s} {2 \ pi v_m} \ neg {arequation *}$

上述等式表示峰值到峰值输出电压摆动等于DC输出电压范围的最高频率。换句话说，它是最大频率 $f_m$ 放大器产生一个不失真的输出。它被称为全功率带宽．它有时也被描述为超级速率限制带宽．

转换速率计算

需要操作放大器以在20kHz的频率下放大具有5伏的峰值电压的信号。找出转换速度。

给定数据： $V_m = 5伏$ ， $f_m = 20khz.$

$\ begin {align *} \ begin {split}＆s = 2 \ pi f_m v_m \\＆= 2 * 3.14 * 20 * 10 ^ 3 * 5 \\＆= 628 * 10 ^ 3 \\＆s = 628000 v / s\，\或\，\，0.628 v / \ mu s \ neg {split} \ neg {align *}$

回转速率的应用

回转速率的一些应用包括:

在乐器中，弹簧电路用于从一个音符向另一个音符提供滑块（也称为滑行或滞后）。
旋转电路用于控制电压在一段时间内缓慢地转换到不同的值。
在某些需要速度和输出需要在一段时间内改变的电子应用中，使用软件生成的回转功能或回转电路。