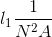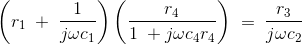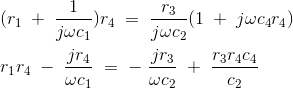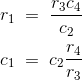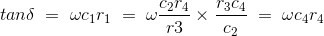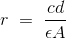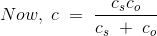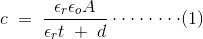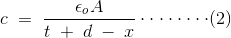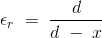先灵桥用先灵桥测量电容

西林电桥理论

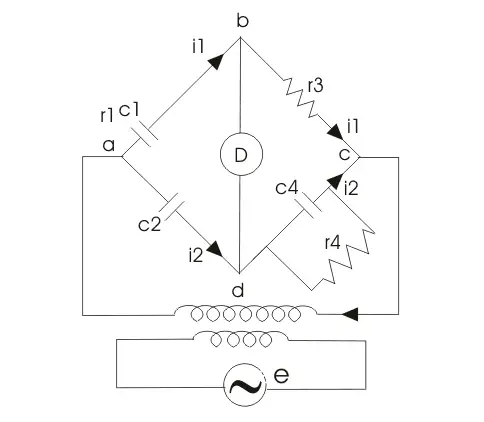
这座桥用于测量到电容对电容器、损耗因子和相对介电常数的测量。让我们考虑一下西林电桥如下所示: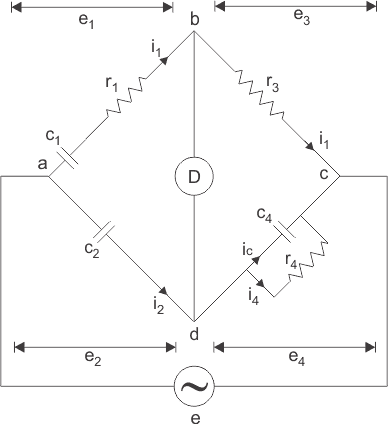
在这里,c₁是否用串联电阻r来确定未知电容的值₁．

c₂是标准电容器。
c₄为可变电容器。
r_3.是一个纯电阻器(即非归纳性质)。
和r₄可变无感电阻是否与可变电阻并联电容器c₄．现在供应给a点和c点之间的电桥。检测器连接在b点和d点之间。

代入z的值₁, z₂, z_3.和Z.₄在上面的方程中，我们得到

把实部和虚部等价，然后分离得到，

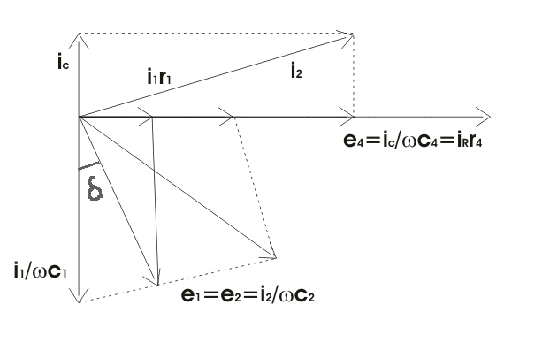
让我们考虑上述雪灵桥电路的相量图并标记电压滴穿过ab bc cd AD，得到e₁e_3.e₄和E.₂分别。由上面的先灵桥相量图，我们可以计算tanδ的值，也称为耗散因子。

我们上面导出的等式非常简单，并且可以容易地计算耗散因子。现在我们将详细讨论高压Schering桥梁。正如我们所讨论的那样，简单的Schering桥（使用低电压）用于测量耗散因子，电容和测量绝缘材料等绝缘油等的其他性能。高压Schering桥的需要是什么？这个问题的答案非常简单，对于测量小电容，我们需要施加高电压和高频，与遭受许多缺点的低电压相比。让我们讨论这种高压Schering桥的更多功能：

1. 电桥臂ab和ad仅由下面给出的电桥所示的电容器组成，这两个电桥的阻抗与bc和cd的阻抗相比相当大。电桥臂bc和cd包含电阻r_3.并并联电容器c₄和电阻r₄分别。由于bc和cd的阻抗相当小，因此bc和cd的阻抗下降也很小。点c接地，因此横跨bc和直流的电压比点c高几伏特。
2. 高电压供应从a变压器该电桥的检波器为振动电流计。
3. 臂ab和ad的阻抗非常大，因此该电路吸引的电流小，功率损耗低，但由于这个低当前的我们需要一个非常灵敏的探测器来检测这种低电流。
4. 固定标准电容器c₂具有压缩气体，其用作介电因此耗散因子可以为压缩空气中的零。接地屏幕放置在桥的高臂和低臂之间，以防止由于电容互连引起的误差。

让我们研究先灵电桥是如何测量相对介电常数的:为了测量相对介电常数，我们首先需要测量一个以样品为介质的小电容器的电容。从这个测量的电容相对电容率值可以很容易地用非常简单的关系式计算出来:

其中，R是相对渗透性。
C为试样作为介质时的电容。
D为电极之间的间距。
A是电极的网区域。
ε为自由空间介电常数。
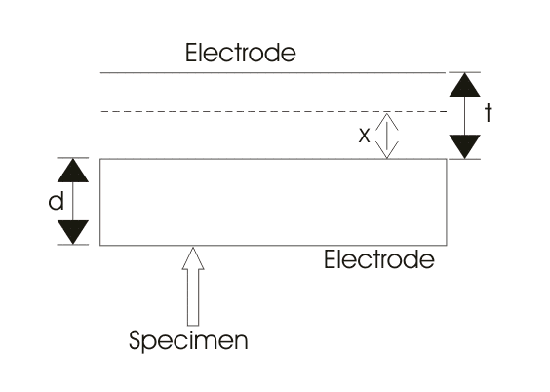
还有一种通过改变电极间距来计算样品相对介电常数的方法。让我们考虑下图

这里A是电极的面积。
D是标本的厚度。
T是电极和样本之间的间隙（这里，该间隙通过压缩气体或空气填充）。
c_年代为样品的电容。
c_o为由于电极和试样之间的间距而产生的电容。
C是C的有效组合_年代和c_o．

由上图可知，当两个电容器串联时，

ε_o自由空间介电常数是ε吗_r当我们去除样品和调整间距使其具有相同的电容值时，电容的表达式是否降为

将(1)和(2)等价，得到ε的最终表达式_r为: