在传输线上落下：它是什么？（以及如何计算它）

传输线的凹陷是什么？

在一个传输线那s被定义为支持点之间的垂直差异（最常见传动塔）和最低点导体。在传输线中的凹凸和张力的计算取决于架空导体的跨度。

调用具有相同级别的跨度（即相同高度的塔）水平跨度。相反，当跨度的支持水平不等时，这被称为不平等的跨度。

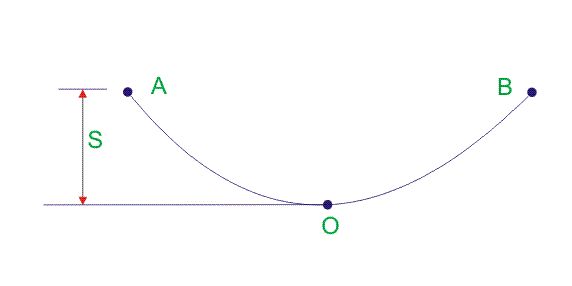
考虑一个传输线导体AOB在级别之间自由悬挂在相同级别（相等跨度）的A和B之间。导体的形状是抛物线，导体的最低点是O.

在上面的架空导体AOB中，S是垂直测量时的下垂。

为什么在传输线导线中是不强制性的？

下垂是强制性的传输线导体悬浮液。导体在两个支架之间附有完美的凹陷值。

这是因为它保护导体免受过度的张力。为了允许导体中安全的张力水平，导体没有完全拉伸;相反，他们被允许追逐。

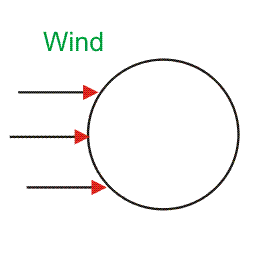
如果是导体在安装过程中完全拉伸，风向导体上施加压力，因此导体有机会从最终支持中拆卸或拆卸。因此s允许在导体悬架期间具有。

有些重要观点：

1. 1. 当相同的平整两个支撑件保持导体时，导体中出现弯曲形状。对于导体的跨度而非常小。
   2. SAG跨度曲线是抛物线。
   3. 导体的每个点的张力总是相切的。

1. 同样，导体的张力的水平分量在导体长度的恒定中是恒定的。
2. 支撑件处的张力几乎等于导体中任何点的张力。

如何计算传输线中的凹陷

在传输线中计算凹陷时，需要考虑两个不同的条件：

1. 当支持处于相同的级别时
2. 当支持不等于等级时

基于支持水平（即，保持架空导体的传输塔）的条件来计算SAG的公式改变。

支持的SAG计算是等级的

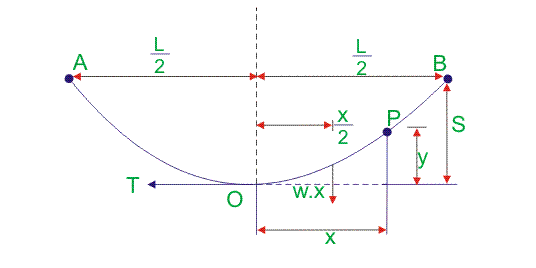
假设，AOB是指挥。A和B是支持点。点O是最低点和中点。
让，L =跨度的长度，即ab
W是导体的每单位长度的重量
T是导体中的张力。
我们选择了导体上的任何一点，比如Point P.
点P从最低点O的距离为o是x。
Y是点O到Point P的高度。

根据上面的图，等于两次关于点O的两个力矩。


支持的SAG计算属于不等程度

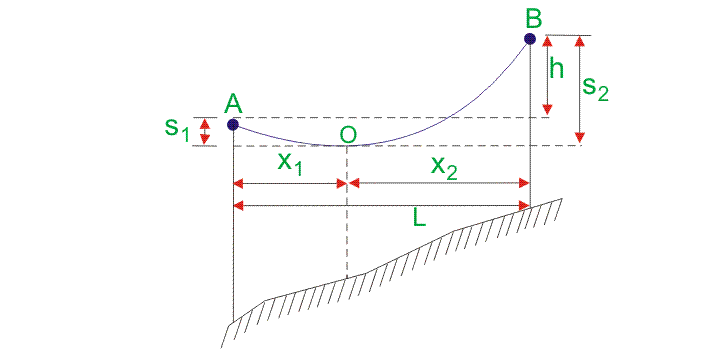
假设AOB是指数的指数作为最低点的指数。
l是导体的跨度。
h是两个支持之间的高度级别的差异。
X₁是较低级别A来自O的支撑距离。
X₂是从O的上层B的支撑距离。
T是导体的张力。
W是导体的每单位长度的重量。
现在，


所以，计算出x的值₁和X.₂，我们很容易找出SAG S的价值₁和sags₂。

上述公式用于计算凹陷时导体在空气中，环境温度正常。因此，导体的重量是其自身的重量。

冰和风在下垂有什么影响？

冰和风对凹凸的一些影响包括：

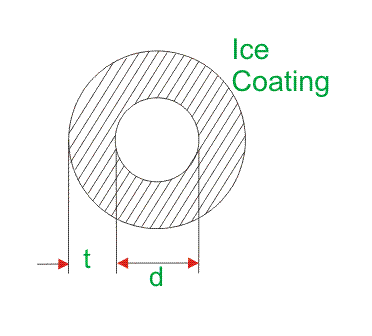
• 当风吹在导体上的某个力和冰周围围绕导体时，导体的每单位长度的重量被改变。
• 风力作用在导体上以在气流方向上水平地改变每单位长度的导体自重。
• 冰装作用在导体上，以垂直向下更改每单位长度的导体自重。
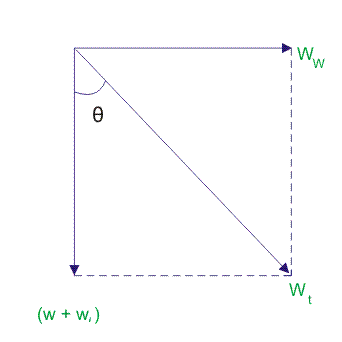
• 考虑一次，导体每单位长度将具有所得重量的风力和冰加载。
• 所得到的重量将与冰载下的冰造成一定角度。

让我们假设，W是每单位长度的导体的重量。
W._一世是每单位长度的冰的重量
W._一世=每单位长度冰×冰量的密度


W._W.是每单位长度的风力
W._W.=每单位面积的风压×每个单位长度的投影区域


因此，每单位长度的导体总重量是


导体中的凹陷由

所以垂直凹陷