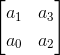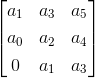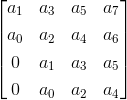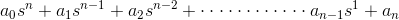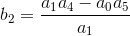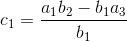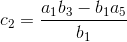ruth Hurwitz稳定标准

阅读理论后网络合成很容易说系统的任何极都分布在 s平面源右侧 使系统不稳定基于条件AHurwitz和E.J.Routh开始调查系统稳定的必要和充分条件将讨论两条标准 系统稳定优先标准由A提供Hurwitz和此标准也被称为Hurwitz稳定标准或ruth Hurwitz稳定标准.

Hurwitz标准

使用特征方程帮助, 我们将制作数赫维兹决定因素 以查找系统稳定性我们定义特征方程系统

现在有n决定因素n^线程顺序特征方程

let we see how we can write决定因素 从特征方程系数逐步程序k^线程顺序特征方程写法如下:
确定性一:a提供此判定值_一号哪里a_一号s系数^N-1特征方程
确定二:值此判定由

内积元素数等同判定数, 我们这里的判定数为二第一行由前二奇系数组成第二行由前二偶系数组成
三确定性:值此判定由

内积元素数等同判定数, 我们这里的判定数为三第一行由前三位奇系数组成,第二行由前三位偶系数组成,第三行由前三位偶系数组成,第一元素零组成,其余二元素二成前两位奇系数
四确定性:值此判定由

内积元素数等同判定数, 我们这里的判定数为四第一行由前三位四系数组成,第二行由前四偶系数组成,第三行由第一元素零组成,其余三元素作为前三位奇系数组成,第四行由第一元素零组成,其余三个元素作为前三位偶系数

通过同样的程序,我们可以泛化决定因素编译总体判定形式如下:

现在为检查以上系统稳定性,计算每个决定因素的值系统稳定时并仅在每个判定值大于0时,即每种判定值应该是正数所有其他情况系统都不稳定

ruth稳定标准

本标准也被称为修改Hurwitz标准系统稳定性我们将分两部分研究这一标准第一部分覆盖系统稳定性的必要条件,第二部分覆盖系统稳定性的充分条件让我们再次把特征方程看成系统

第一部分(系统稳定性的必要条件):在此,我们有两个条件写法如下:

1. 特征方程所有系数应该是正值和实值
2. 特征方程所有系数应非零

第二部分(系统稳定条件充足):先搭建路由数组构造路由数组

• 第一行由特征方程所有偶数组成从上到下排列(偶至)第一行写法如下:₀a/₂a/₄a/₆...
• 第二行由特征方程所有奇特条件组成顺序排列从优先词移到最后词移第一行写法如下:_一号a/₃a/₅a/₇...
• 三行元素计算方式如下:
  第一元素乘法a₀下列对角元素a/₃)从 a产品中减去_一号和₂中位₂下列对立元素)并最后除法结果_一号.数学学上我们写为第一元素

第二元素乘法a₀相向元素相邻列(即二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/a/₅)从 a产品中减去_一号和₄地点,a₄相邻列对立元素)并最后除法结果_一号.数学方面,我们写为二元

类似地,我们可以计算第三行所有元素
第四行元素可用下列程序计算:
第一元素乘法b_一号下列对角元素a/₃)从 a产品中减去_一号和b₂地点b₂下列对立元素)并最后除法结果_一号.数学学上我们写为第一元素

第二元素乘法b_一号相向元素相邻列(即二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/二维列/a/₅)从 a产品中减去_一号和b₃地点b₃相邻列对立元素)并最后除法结果_一号.数学方面,我们写为二元

类似地,我们可以计算第四行所有元素
类似地,我们可以计算所有行的所有元素
稳定标准,如果第一列所有元素均正则系统将稳定系统将不稳定
现有一些与Routh稳定标准有关的特殊案例下文讨论

案例一数组中任意行的第一个术语为0,而其余部分至少有一个非零术语
假设极小值(++++++++0+0+0+0++0++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++将0替换为routh数组所有元素计算所有元素后,我们将对包含(+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++解决每个元素的限值时,如果我们得到正限制值,我们将表示给定系统在其他条件中稳定

案例二当 Routh数组中任意行的所有元素为零时在这个例子中,我们可以说系统有边缘稳定性的征兆先让我们理解拥有行所有元素零的物理意义物理意义是 s平面特征方程有对称定位根现在为求稳定处理此案例 我们先找出辅助方程辅助方程可使用行数略高于routh数组零数行组成寻找辅助方程后,我们将区分辅助方程获取零行元素假设新路由数组没有改变符号使用辅助方程, 并在此表示给定系统有限稳定而在所有其他例子中,我们会说给定系统不稳定