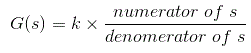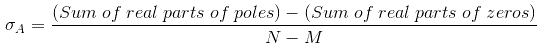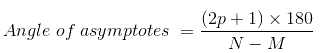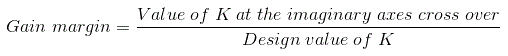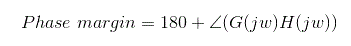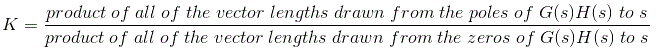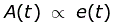的控制系统中的根位点技术是埃文斯在1948年首次提出的。任何物理系统都可以用传递函数表示,其形式为
我们可以从G(s)中找到极点和零点。极点和零点的位置是保持视场稳定、相对稳定、瞬态响应和误差分析的关键。系统投入服务时发生杂散电感和电容进入系统,从而改变极点和零点的位置。在控制系统中的根位点技术我们将评估根的位置,它们的运动轨迹和相关信息。这些信息将用于评论系统性能。
现在,在我介绍什么是根轨迹技术之前,很有必要在这里讨论一下这个技术相对于其他稳定性标准的一些优势。根轨迹技术的一些优点写在下面。
根位点技术的优点
- 与其他方法相比,根位点技术在控制系统中易于实现。
- 借助根轨迹,我们可以轻松预测整个系统的性能。
- 根轨迹提供了更好的方式来指示参数。
现在有各种与root轨迹技术相关的术语,我们将在本文中经常使用。
- 与根基因座技术相关的特征方程:1 + G(s)= 0被称为特征方程。现在在区分特征方程和等式DK / DS等于零的情况下,我们可以脱离点。
- 突破点:假设从杆开始的两个根基因座并且在相反的方向上移动彼此碰撞,使得在碰撞之后,它们以对称的方式开始以不同的方向移动。或者发生特征方程的多根根的分离点(S)= 0。k的值在根基因座分裂的分支突破的点处最大。突破点可能是真实的,虚构的或复杂的。
- 断点:休息的条件在图上写在图表上面:
根轨迹必须存在于真实轴上的两个相邻零之间
.
- 重心:它也被称为质心,被定义为所有渐近线开始的点。数学上,它是由传递函数中极点和零的和的差除以总极点数和总零数的差来计算的。重心总是实的,用σ表示一个.
其中,n是极点,m是零的数量。 - 根轨迹渐近线:渐近源自重心或质心源自重心,并以明确的角度走向无限。渐近当他们脱离点点时向根轨迹提供方向。
- 渐近角度:渐近线与实轴成一个角这个角可以从给定的公式中计算出来,
其中,p = 0,1,2 .......(N-M-1)
N是极点的总数
m是零的总数。 - 到达或离开的角度:计算了系统中存在复极时的离角。出发角可以计算为180-{(从其他极点到一个复极的角度之和)-(从零点到一个复极的角度之和)}。
- 具有虚构轴的根基因座:为了求出根轨迹与虚轴的交点,必须采用Routh Hurwitz准则。首先,我们找到辅助方程,然后相应的K值将给出交点的值。
- 增益裕度:我们定义增益裕度,在系统变得不稳定之前可以乘以增益因子的设计值。在数学上,它由公式给出
- 阶段保证金:相余量可以从给定的公式计算:
- 根轨迹对称性:根轨迹对对称的X轴或实轴对称。
如何在根基因座上的任何点确定k的值?现在有两种方法可以确定k的值,下面描述k。
- 幅度标准:在根轨迹上的任意点,我们可以应用大小标准,
利用这个公式,我们可以计算任意点的K值。 - 使用根位点图:K在根轨迹上任意s处的值是
根轨迹图
这在控制系统中也称为根轨迹技术,用于确定给定系统的稳定性。现在为了用根轨迹法确定系统的稳定性,我们找到了K值的范围,在这个范围内系统的完全性能是令人满意的,运行是稳定的。
现在有一些结果应该记住,以绘制根轨迹。这些结果如下所示:
- 根轨迹所在区域:在平面上绘制所有杆和零后,我们可以通过使用下面写入的简单规则轻松找到根轨迹的存在区域,
只有那段段在制作根轨迹时,如果段右侧的杆子和零是奇数的杆和零的总数。 - 如何计算单独的根基因座的数量?:如果根的数目大于极点的数目,则单独的根位点的数目等于根的总数,否则,如果根的数目大于零的数目,则单独的根位点的数目等于极点的总数。
绘制根轨迹的过程
把这些要点记在心里,我们就能画出根轨迹图对于任何类型的系统。现在让我们讨论制作根轨迹的程序。
- 从开环传递函数中求出所有的根和极点,然后在复平面上绘图。
- 所有的根轨迹从k = 0的极点开始,在k趋于无穷时的零点结束。终止于无穷远处的分支数等于G(s)H(s)的极点数与零点数之差。
- 在找到M和N的值后,从上述方法中找到根基因座的存在区域。
- 如果有的话,计算断裂点并分解点。
- 通过计算渐近线的斜率,在复平面上绘出根轨迹的渐近线和质心。
- 现在计算出发角和根轨迹与虚轴的交点。
- 现在用我上面描述的任何一种方法来确定K的值。
通过上面的过程,您可以轻松地画出根轨迹图对于任何开环传输功能。
- 计算增益边际。
- 计算相余量。
- 你可以很容易地通过使用Routh数组来评价系统的稳定性。