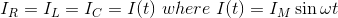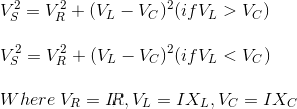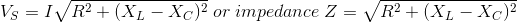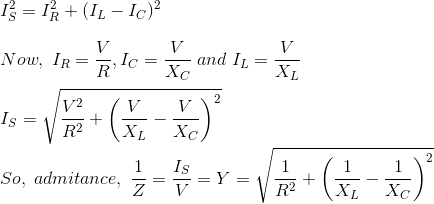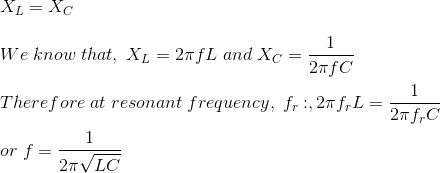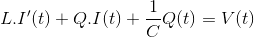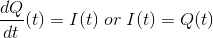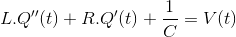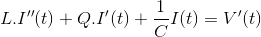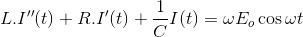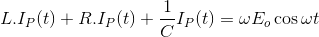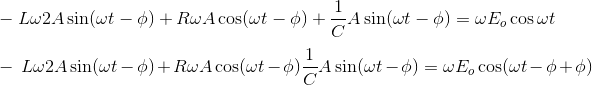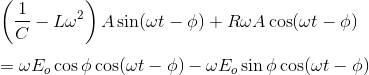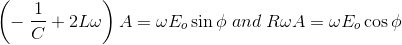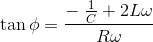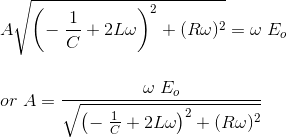在一个RLC电路, a的最基本元素电阻器,电感器,电容器都是通过电压供应。所有这些元素在本质上都是线性和被动的。无源元件是消耗能源而不是生产能源的能源;线性元件是指电压与电压之间具有线性关系的元件当前的.
有许多方法连接这些元件跨电压电源,但最常见的方法是串联或并联这些元件。的RLC电路与LC电路的谐振特性相同,但与LC电路相比,由于电路中存在电阻,振荡很快消失。
系列RLC电路
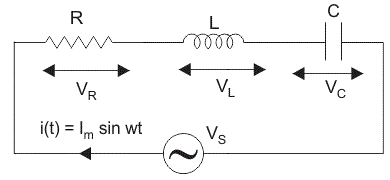
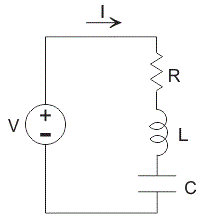
当电阻器、电感器和电容与电压源串联时,就称为这样形成的电路系列RLC电路.
由于所有这些元件是串联的,所以每个元件的电流保持不变,
让VR为两端电压电阻器, R。
Vl为两端电压电感器, L。
VC为两端电压电容器C。
Xl是归纳电抗.
XC是容性电抗。
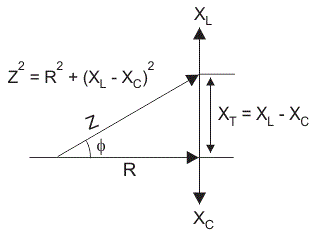
RLC电路中的总电压不等于通过电阻、电感和电容的电压的代数和;但它是一个矢量和,因为在电阻的情况下,电压和电流是同相的,对于电感,电压超前电流90o对于电容器来说,电压比电流落后90o(根据冰人艾利).
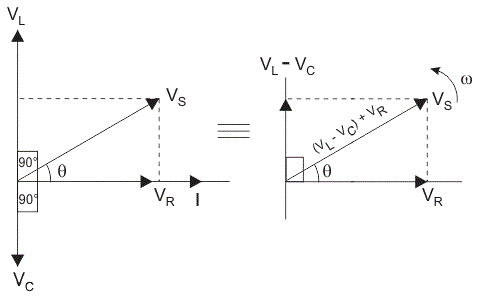
所以,每个分量的电压不是同相的;所以它们不能算数相加。下图是串联RLC电路的相量图。在绘制RLC串联电路的相量图时,以电流为参考,因为串联电路中各元件的电流保持不变,且各元件的电压矢量是参照共同电流矢量绘制的。
串联RLC电路的阻抗
串联RLC电路的阻抗Z被定义为对应电路电流的反方向电阻R,感抗,Xl和容抗XC.如果感抗大于容抗,即Xl> XC,则RLC电路具有滞后相角,如果容抗大于感性抗即XC> Xl然后,RLC电路有超前相位角,如果电感和电容相同,即Xl= XC那么电路就会表现为纯电阻电路。
我们知道
在那里,
替换的值
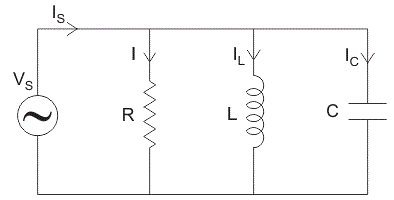
并联RLC电路
在并联RLC电路电阻、电感和电容在电压源上并联。并联RLC电路与串联RLC电路完全相反。施加的电压在所有组件上保持相同,并且供应电流被分割。
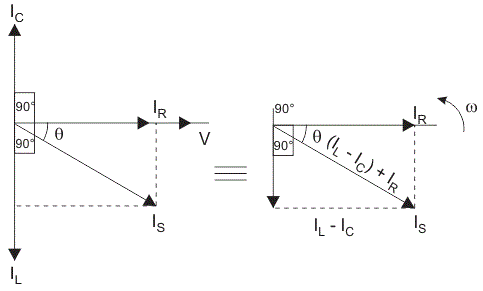
总电流的供应不等于数学和电流的各个组件,但是它等于矢量和电流,电流在电阻、电感和电容不是彼此在同一阶段;所以它们不能算数相加。
并联RLC电路的相量图R为流过电阻的电流,R单位为安培。
我C为流过电容器的电流,单位为安培。
我l为流过电感的电流,单位为L安培。
我年代为电源电流,单位为安培。
在并联RLC电路中,所有元件并联连接;所以每个元件上的电压是相同的。因此,在绘制相量图时,以电压为参考矢量,所有其他电流即电压R,我C,我l是相对于这个电压矢量的。通过每个元素的电流可以使用基尔霍夫电流定律,表示进入一个结或节点的电流之和等于离开该节点的电流之和。
如上所示的阻抗方程中,Z为并联RLC电路;每个元件都有阻抗的倒数(1 / Z)即。导纳所以在并联RLC电路中,用导纳代替阻抗是很方便的。
RLC电路中的谐振
在一个包含电感和电容的电路中,能量以两种不同的方式存储。
- 当电流在电感器中流动时,能量就储存在电感器中磁场.
- 当电容器充电时,能量储存在静电场中。
电感中的磁场是由放电电容提供的电流形成的。同样,电感器磁场坍缩产生的电流对电容器充电,这个过程不断进行,导致电能在磁场和电场之间振荡。在某些情况下,在被称为谐振频率的特定频率下,电路的感应电抗与电容电抗相等,从而导致电能在电容的电场和电感的磁场之间振荡。这就形成了一个谐波振荡器为电流。在RLC电路,电阻器的存在使这些振荡在一段时间后消失,称为电阻器的阻尼效应。
谐振频率公式
在共振时,在某一频率称为共振频率fr.
当谐振发生时,电路的感抗与容抗相等,使得串联RLC电路的电路阻抗最小;但当电阻、电感和电容并联时,电路阻抗最大,因此并联RLC电路有时被称为反谐振器。请注意,振动物体的最低共振频率称为它的共振频率基频
串联RLC电路与并联RLC电路的区别
| S.NO | RLC串联电路 | RLC并联电路 |
| 1 | 电阻、电感和电容是串联的 | 电阻、电感和电容是并联的 |
| 2 | 电流在每个元素中是相同的 | 电流各元素不同,总电流等于各支路电流的矢量和,即I年代2=我R2+(我C——我l)2 |
| 3. | 所有元件的电压是不同的,总电压等于每个元件电压的矢量和,即V年代2= VR2+ (Vl- - - - - - VC)2 | 每个元件的电压保持不变 |
| 4 | 在绘制相量图时,以电流为参考矢量 | 在绘制相量图时,以电压为参考矢量 |
| 5 | 每个元件的电压由:V给出RV =红外,lX =我l, VCX =我C | 每个元素的Current是: 我R= v / r, IC= v / xC,我l= v / xl |
| 6 | 使用阻抗计算更方便 | 使用导纳计算更方便 |
| 7 | 在共振时,Xl= XC时,电路具有最小阻抗 | 在共振时,Xl= XC时,电路具有最大阻抗 |
RLC电路方程
考虑一个RLC电路电阻R、电感L和电容C串联,由a驱动电压源V.设Q为电容上的电荷,流过电路的电流为i基尔霍夫电压定律
在这个方程;阻力,电感,电容电压是已知的量,而电流和电荷是未知的量。我们知道电流是电荷流动的速率,所以它是由
再次微分I'(t) = Q " (t)
对上面的方程对t求导,我们得到,
t = 0时,V(0) = 0 t = t时,V(t) = Eo罪ωt
对t微分得到V'(t) = ωEo因为ωt
将V'(t)的值代入上式
假设这个方程的解是IP(t) = Asin(ωt - ǿP(t)是上述方程的解,那么它必须满足这个方程,
现在代入I的值P对t求导,得到,
用cos (A + B)的公式结合类似的项,
把sin(ωt - φ)和cos(ωt - φ)的系数在等式两边匹配,
现在我们有两个方程和两个未知数,即φ和A,通过除以这两个方程,
对等式进行平方和相加,就得到
基于拉普拉斯变换的RLC电路分析
步骤1:画出给定电路的相量图。
步骤2:利用RLC串联电路中的基尔霍夫电压定律和RLC并联电路中的电流定律,建立时域微分方程。
步骤3:使用拉普拉斯变换将这些微分方程从时域转换到s域。
步骤4:为求未知变量,请解这些方程。
步骤5:应用拉普拉斯逆变换将方程从s域转换到时域。
RLC电路的应用
它被用作低通滤波器,高通滤波器,带通滤波器带阻滤波器,电压乘法器和振荡器电路。用于收音机或音频接收机的调谐。