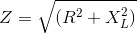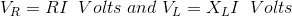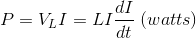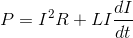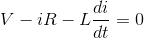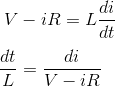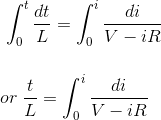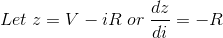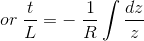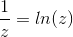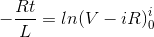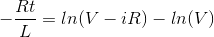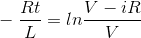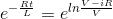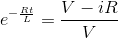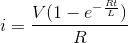RL系列电路分析（Phasoraik，示例和推导）

什么是RL电路？

RL电路（也称为RL滤波器或RL网络）被定义为一个电路由它组成被动电路元件A.电阻器（r）和一个电感器（l）通过a驱动连接在一起电压源或者目前的来源。

由于存在电阻器在电路的理想形式中，RL电路将消耗能量，类似于一个RC电路或者RLC电路。

这与理想形式不同LC电路，由于缺乏电阻，这将不会消耗能量。虽然这只是电路的理想形式，并且在实践中，即使是LC电路也会因为非零而消耗一些能量抵抗性部件和连接线。

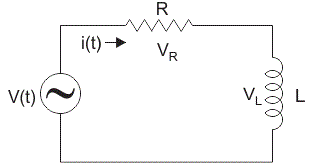
考虑一个简单的RL电路电阻器，R和电感器，L与a串联连接电压供应V伏特。让我们思考当前的在电路中流动是I（放大器）和电流通过电阻器和电流电感器是I._R.和我_L.分别。从两者起来抵抗性电感器串联连接，因此元件和电路中的电流保持不变。即我_R.= I._L.= I.让V_R.和V._L.是电压下降跨电阻和电感。

申请Kirchhoff电压法（即电压降的总和必须等于施加电压）到我们得到的这次电路，

RL电路的相量图

在绘制之前Phasor图系列RL电路，在电阻和电感器的情况下，应该知道电压和电流之间的关系。

1. 1. 电阻器
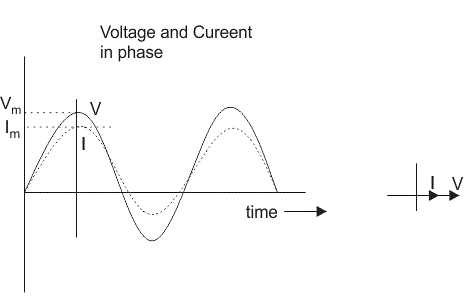
      在电阻器的情况下，电压和电流在相位相位或者可以说电压和电流之间的相角差为零。

1. 1. 电感器
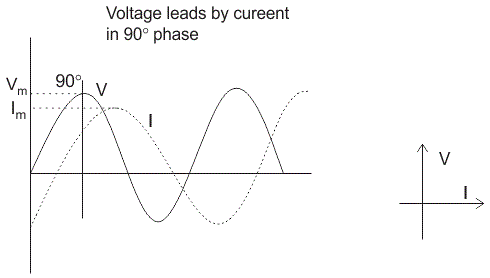
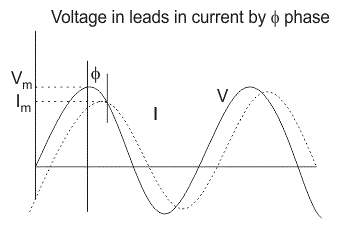
      在电感器中，电压和电流不相位。电压导致电流的90^O.或者换句话说，电压达到其最大值和零值90^O.在当前达到它之前。

1. RL电路
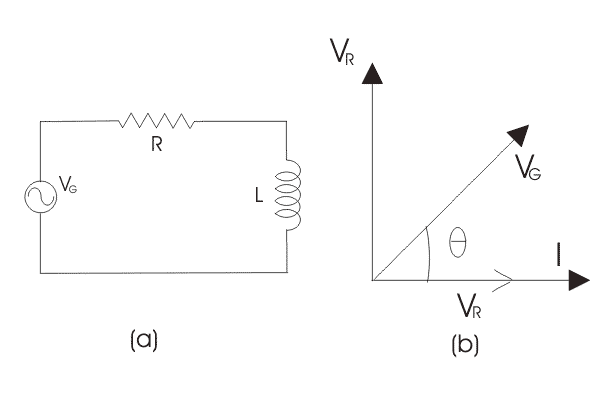
   用于绘制系列RL电路的相位图;按照以下步骤操作：

继 - 我在RL电路系列的情况下，电阻和电感器串联连接，因此电流在两个元件中流动相同I.E i_R.= I._L.= I.因此，将当前的相量作为参考，并如图所示的水平轴上将其绘制。
第一次。在电阻器的情况下，电压和电流都处于相同阶段。所以绘制电压量量值，v_R.沿着相同的轴或方向作为当前相量的相同。I.E V._R.与I相同。

第三次。我们知道在电感器中，电压引线电流为90^O.，绘制v_L.（跨电感器的电压降）垂直于当前相量。
步骤 - iv。现在我们有两个电压v_R.和V._L.。绘制所得载体（v_G）这两个电压。如，
从直角三角形，我们得到，相位角


结论：在纯电阻电路的情况下，电压和电流之间的相位角为零，在纯电感电路的情况下，相位角为90^O.但是当我们结合两个电阻和电感时，串联RL电路的相位角在0之间^O.到90.^O.。

RL电路系列的阻抗

这阻抗串联RL电路反对交流电流的流动。RL电路的阻抗只不过是抵抗（R）的结合效应归纳电抗（X_L.）作为整体的电路。欧姆中的阻抗Z由，
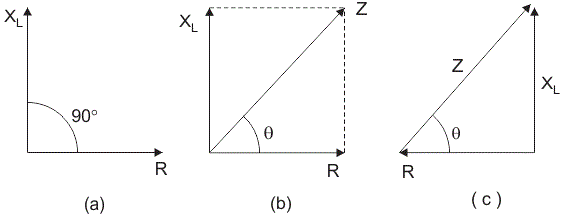
z =（r²+ X._L.²）^0.5并且从直角三角形，相位角θ=棕褐色^{- 1}（X_L./ r）。

系列RL电路分析

在串联RL电路中，频率f，电压V，电阻r和电感L是已知的，没有用于直接测量感应电抗和阻抗的值的仪器;因此，为了完全分析RL电路，请遵循这些简单的步骤：

步骤1。由于频率和电感器的值是已知的，因此首先计算电感电抗的值x_L.： X_L.=2πfl欧姆。
第2步。从x的值_L.和r，计算由提供的电路的总阻抗

第3步。计算电路θ=棕褐色的总相角^{- 1}（X_L./ r）。
第四步。用欧姆的法律并找到总电流的值：i = v / z放大器。
第5步。通过使用欧姆的法律计算电阻器R和电感L的电压。由于电阻和电感器串联连接，因此它们中的电流保持不变。

在RL电路中的电源

在串联RL电路中，有些能量被电阻器消散，并且某些能量被交替存储并由电感返回

1. 瞬时电力提供电压源v是p = vi（瓦特）。
2. 电阻以热量的形式散发出电源，p = i²r（瓦特）。
3. 能量存储在电感器中的速率，

因此，通过添加电阻散发的功率和由电感器吸收的功率来给出串联RL电路的总功率。

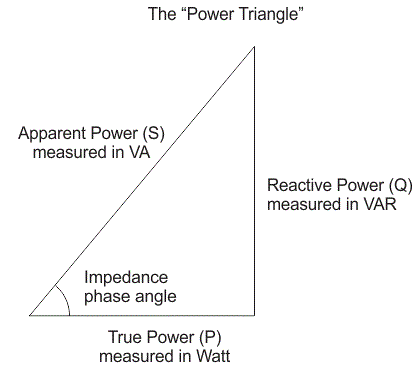
串联RL电路的电源三角形如下所示，

这电力因数COSθ被定义为真正功率与表观功率的比率。

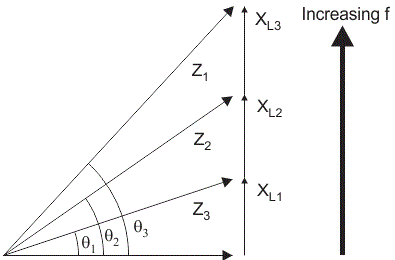
频率阻抗和相位角的变化

上图显示了阻抗三角形。该阻抗三角形的基础代表抵抗性。电阻与频率无关;因此，如果频率增加或减小，电阻保持恒定。归纳抵抗的公式是x_L.=2πfl。所以，如果频率增加，电感式电抗x_L.还增加并且如果电感电抗增加，电路的总阻抗也会增加，这导致相位角θ的变化具有频率。因此，在串联RL电路中，如果频率增加，

1. 由于它与频率成正比成比例而增加，电感抗抵抗也会增加。
2. 总阻抗Z增加。
3. 相角θ增加。
4. 抵抗性保持不变。

串联流动流动电流的表达式

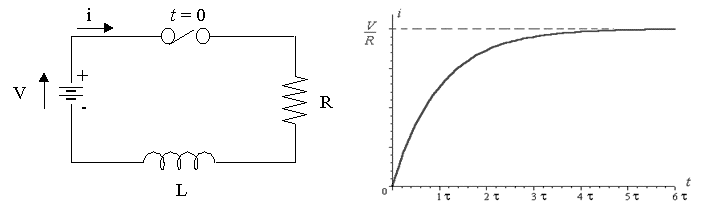
考虑一种电路，其中电阻与电感器串联连接电压源V伏特，应用于其中。最初开关打开。L.et us say at time ‘t’ we close the switch and the current ‘i’ starts flowing in the circuit but it does not attains its maximum value rapidly due to the presence of inductor in the circuit as we know inductor has a property to oppose the change in the current flowing through it.

在上面的RL电路中应用Kirchhoff的电压法，

重新排列上述等式，

我们得到，

现在使用替代方法整合右手边，

取代我们得到的值，

我们知道融合，

所以我们得到，

通过应用我们得到的限制，

再次简化，

在双方服用​​安提戈，

我们知道e^{ln x.}= x，所以我们得到，

在我们得到的一边移动“我”的术语，

等式中的术语L / R称为时间常数，（τ）RL系列电路，并且它定义为电流达到其最大稳态值的时间，术语v / R表示电路中电流的最终稳态值。