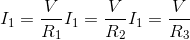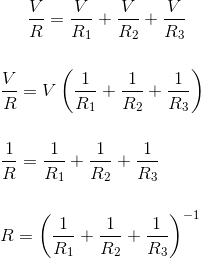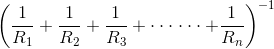平行串联和电阻的电阻

超过一个电阻除此之外，可以串联或并联连接，两个以上的电阻也可以与串联和平行组合连接。在这里，我们将主要讨论系列和并联组合。

系列抗性

假设你有三个不同电阻类型- R₁，R.₂和R._3.- 并且您将它们结束结束，如下图所示，那么它将被称为电阻串联。在串联连接的情况下，组合的等效电阻是这三个电阻的总和。
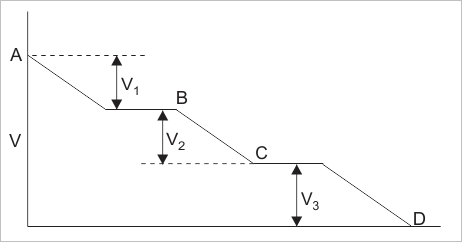
这意味着，下图中的点A和D之间的电阻等于三个单独电阻的总和。这当前的进入到组合的A点，也将从D点离开，因为在电路中没有提供其他并行路径。

现在说这个当前是我。所以这个目前我将通过阻力r₁，R.₂和R._3.。申请欧姆的法律，可以找到电压降在抵抗力将是v₁= IR.₁，V.₂= IR.₂和V._3.= IR._3.。现在，如果总数电压应用于跨越的组合电阻串联，是V.
然后显然

由于，跨各个电阻的电压降的总和仅为相同的组合施加电压。

现在，如果我们认为电阻的总组合为单个电阻器电阻值R，然后根据欧姆的法律，
v = Ir ............（2）

现在，比较方程（1）和（2），我们得到

因此，上述证据表明，串联电阻组合的等效电阻等于单个电阻的总和。如果有n个电阻而不是三个电阻，则相当于电阻

平行抗性

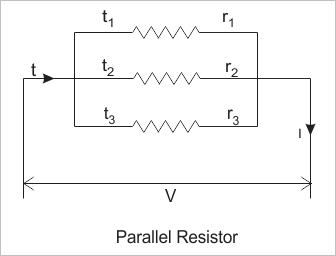
说我们有三个电阻值r₁，R.₂和R._3.。这些电阻器以这样的方式连接，即每个电阻器的右侧和左侧端子连接在一起，如下图所示。

调用这种组合平行抗性。如果电势差应用于这种组合，然后它将绘制一个电流i（例如）。
由于此目前将通过这三个并行路径电阻，电流将分为三个部分。说电流我₁， 一世₁和我₁通过电阻器₁，R.₂和R._3.分别。
总源电流的地方

现在，从这个图中，很清楚，每个都是平行抗性，相同的连接电压源， 这电压降在每个电阻相同，它与电源电压v相同（例如）。
因此，根据欧姆的法律那


现在，如果我们认为组合的等效电阻是R.
然后，
现在放置我的价值，我₁， 一世₂和我_3.在等式（1）中我们得到，

上述表达式表示平行电阻的等同电阻。如果有n个平行连接的电阻，而不是三个电阻，则相当于电阻的表达将是