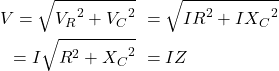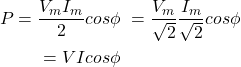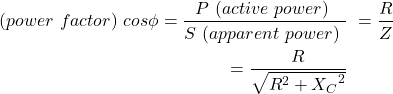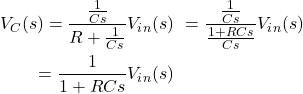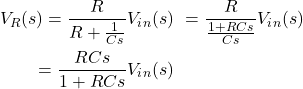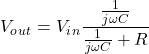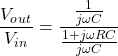RC电路分析:串联&并联(explain in Plain English) | Electrical4Ubetway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是RC电路?

RC电路（也称为RC滤波器或RC网络）代表电阻电容器电路。RC电路定义为电路组成的被动电路组件的电阻器(R)和电容器答案:C电压源或者目前的来源．

由于在电路的理想形式中存在一个电阻，RC电路将消耗能量，类似于RL电路或者RLC电路．

这与理想形式不同LC电路，由于缺乏电阻，这将不会消耗能量。虽然这只是电路的理想形式，并且在实践中，即使是LC电路也会因为非零而消耗一些能量电阻部件和连接线。

系列RC电路

在RC系列电路中，具有纯电阻电阻欧姆和纯净电容器电容C的法拉第是串联的。

在这里 $我$ 是个均方根值电路中的电流。

$V_R$ 电阻器中的电压是电阻器r。

$V_C$ 电容器C上的电压是电容器上的电压。

$V$ 为电源电压均方根值。

该图显示了串联RC电路的矢量图。

从串联电路电流 $“我”$ 是相同的，所以它被视为参考。

$V_R = IR.$ 用电流绘制 $“我”$ 因为在一个纯粹的电阻器的电压和当前的都是相同的。

$v_c = i x_c$ 牵引与电流滞后吗 $“我”$ 通过 $90 ^ 0$ 因为在一个纯粹的电容器电压和电流是 $90 ^ 0$ 在彼此中，即电压滞后 $90 ^ 0$ 或者电流通过 $90 ^ 0$ ．

现在 $V$ 向量和是什么 $V_R$ 和 $V_C$ ．

$\ \{对齐*}\开始,因此,\ \,V ^ 2 = {V_R} ^ 2 + {V_C} ^ 2 \{对齐*}结束$

${对齐*}\ \开始开始{分裂}V = {\ sqrt {{V_R} ^ 2 + {V_C} ^ 2 }} \ & = {\ √6{{红外}^ 2 + {IX_C} ^ 2}} \ & =我{\√6 {{R} ^ 2 + {X_C} ^ 2}} \ & =工业区\ \{分裂}\{对齐*}结束结束$

的阻抗的R-C串联电路

$\ begin {aligne *} z = {\ sqrt {{r} ^ 2 + {x_c} ^ 2}} \ neg {align *}$

$\ \{对齐*}\开始,,\ \ X_C = \压裂{1}{{\ω}C} = \压裂{1}{2{\π}fC} \{对齐*}结束$

的电压和阻抗三角形如图所示。

如所看到的，矢量 $V$ 滞后 $我$ 一个角度Ø在哪里

$谭\{对齐*}开始{\φ}= \压裂{IX_C}{红外}\{对齐*}结束$

$\ begin {align *} {\ phi} = tan ^ - ^ 1 \ frac {x_c} {r} \ neg {align *}$

因此，在R-C系列电路电流中 $“我”$ 引出电源电压 $“V”$ 由一个角

$\ begin {align *} {\ phi} = tan ^ - ^ 1 \ frac {x_c} {r} \ neg {align *}$

$\ begin {aligne *} \，\，i.e. \，\如果\，\，v = v_m sin {\ oomega} t \ neg {alight *}$

$\开始{对齐*}i = I_m罪({\ω}t +{\φ})结束\{对齐*}$

$\ \{对齐*}\开始,,\ \,I_m = \压裂{V_m} {Z} \{对齐*}结束$

R-C串联电路的电压和电流波形如图所示。

RC串联电路中的功率

的瞬时值权力是瞬时值的乘积吗电压和当前的．

$\begin{align*} P = V I \end{align*}$

$\ begin {对齐*} =（v_m sin {\ omega} t）[i_m sin（{\ omega} t + {\ phi}）] \结束{align *}$

$\ begin {align *} = \ frac {v_m i_m} {2} [2sin {\ omega} t * sin（{\ omega} t + {\ phi}）] \ neg {align *}$

$\ begin {align *} = \ frac {v_m i_m} {2} [cos [{\ omega} t - （{\ omega} t + {\ phi}）] - cos [{\ omega} t +（{\ omega}t + {\ phi}）]] \结束{align *}$

$\ begin {align *} = \ frac {v_m i_m} {2} [cos（{ - \ phi}） - cos（{2 \ omega} t + {\ phi}）] \ neg {align *}$

$\ begin {aligne *} = \ frac {v_m i_m} {2} [cos {\ phi} - cos（{2 \ omega} t + {\ phi}）] \结束{align *}$

$\开始{对齐*}\,\ [,\ \,cos({φ- \})= cosφ{\}\ \,因为\ \,cos \ \,曲线\ \,是\ \,对称),\ \ \最终{对齐*}$

${对齐*}= \ \开始压裂{V_m I_m}{2}因为{\φ}- \压裂{V_m I_m} {2} cos({2ω\}t +{\φ})\{对齐*}结束$

因此瞬时功率由两部分组成。

1.常数部分= $\压裂{V_m I_m}{2}因为{\φ}$

2.一个变化的分量= $\压裂{V_m I_m} {2} cos({2ω\}t +{\φ})$ 这在供应频率的两倍时变化。

在一个完整的周期内，变功率分量的平均值为零。

因此，在一个周期上的RC系列电路中消耗的平均功率是

$\ begin {aligne *} \ begin {split} p = \ frac {v_m i_m} {2} cos {\ phi} \＆= \ frac {v_m} {\ sqrt {2}} \ frac {i_m} {\ sqrt{2}} cos{\phi} \ & = V I cos{\phi} \ \end{split} \end{align*}$

在哪里 $V$ 和 $我$ 是rms值电路中的施加电压和电流。

RC串联电路中的功率因数

考虑表现出的数字权力和阻抗三角形。

$\ begin {align *} \ begin {split} \，\，\，（power \，\，factor）\，\，cos {\ phi} = \ frac {p \，\，（活动\，\，power）\，\，} {s \，\，（明显\，\，power）\，\，} \＆= \ frac {r} {z} \＆= \ frac {r} {\ sqrt {{r} ^2 + {x_c} ^ 2}}}}} \ \ end {split} \ end {align *}$

平行的RC电路

在并行R-C电路中，具有纯电阻电阻 $R$ 在欧姆和纯净电容器的电容 $C$ 在Farads并行连接。

并联RC电路中的电压降是相同的，因此施加的电压等于电阻上的电压和电容上的电压。并联R-C电路中的电流是通过电阻和电容的电流之和。

$\ begin {align *} v = v_r = v_c \ neg {align *}$

$\ begin {align *} i = i_r + i_c \ neg {align *}$

对于电阻器，通过它的电流由欧姆的法律：

$\ begin {align *} i_r = \ frac {v_i_n} {r} \ neg {align *}$

电容器的电压 - 电流关系是：

$\ begin {align *} i_c = c \ c \ frac {dv_i_n} {dt} \ neg {align *}$

申请基尔霍夫电流定律到并联R-C电路

$\begin{align*} I_R + I_C = 0 \end{align*}$

${对齐*}\ \开始压裂{v} {R} + C \压裂{dV} {dt} = 0 \{对齐*}结束$

上面的方程是R-C电路的一阶微分方程。

并联RC电路的传递函数:

$\ begin {对齐*} h（s）= \ frac {v_o_u_t} {i_i_n} = \ frac {r} {1 + rcs} \ end {align *}$

RC电路方程

电容器C表现为a $\压裂{1}{sC}$ 在频域有电压源的 $\压裂{vC(0 ^)}{年代}$ 与它串联在一起 $VC（0 ^ - ）$ 是通过电容器的初始电压。

阻抗：复杂的阻抗, $Z_C.$ 电容器C是

$\begin{align*} Z_C = \frac {1} {sC} \end{align*}$

$\ begin {aligne *} \，\，其中，\，\，s = j {\ omega} \ neg {alpion *}$

$\，\，1。\，\，j$ 表示虚部 $j ^ 2 = 1$

$\，\，2。\，\，\ \ oomega$ 代表正弦角频率（每秒弧度）

$\ begin {aligne *} z_c = \ frac {1} {j \ oomega c} = \ frac {j} {j2 \ omega c} = - \ ommga c} {\ omega c} \ end {align *}$

电流:电流在串联R-C电路中的各处相同。

$\{对齐*}我开始(s) = \压裂{V_i_n (s)} {R + \压裂{1}{Cs}} ={\压裂{Cs} {1 + RCs}} V_i_n结束(s) \{对齐*}$

电压:通过应用分压器规则，电容器上的电压是：

$\ begin {align *} \ begin {split} v_c（s）= \ frac {\ frac {1} {cs}} {{r + \ frac {1} {cs}} v_i_n（s）\＆= \ frac{\ frac {1} {cs} {{\ frac {1 + rcs} {cs}} v_i_n（s）\＆= \ frac {1} {1 + rcs} v_i_n（s）\ \ eN {split} \结束{align *}$

电阻上的电压是：

${对齐*}\ \开始开始{分裂}V_R (s) = \压裂{R} {R + \压裂{1}{Cs}} V_i_n (s ) \ & = \ 压裂{R}{\压裂{1 + RCs} {Cs}} V_i_n (s) \ & = \压裂{RCs} {1 + RCs} V_i_n (s) \ \{分裂}\{对齐*}结束结束$

RC电路电流

电流在R-C电路中的各处相同。

$\{对齐*}我开始(s) = \压裂{V_i_n (s)} {R + \压裂{1}{Cs}} ={\压裂{Cs} {1 + RCs}} V_i_n结束(s) \{对齐*}$

RC电路的传递函数

的传递函数从输入电压到电容两端的电压是

${对齐*}\开始H_C (s) = \压裂{V_C (s)} {V_i_n (s)} = \压裂{1}{1 + RCs} \{对齐*}结束$

类似地，从输入电压转移函数到电阻两端的电压是

$\ begin {align *} h_r（s）= \ frac {v_r（s）} {v_i_n（s）} = \ frac {rcs} {1 + rcs} \ end {align *}$

RC电路的阶跃响应

当电路中某些东西发生变化时，当开关闭合时，电压和电流也会发生变化，以适应新的条件。如果变化是突然的阶跃，则称为阶跃响应。

电路的总响应等于强制响应加自然反应。这些响应可以使用叠加原理结合。

强制响应是电源源导通的响应，但是假定初始条件（内部存储的能量）为零。

自然响应是一种电源关闭，但电路包括初始条件(电容器的初始电压和电感中的电流)。由于电源被切断，自然响应也被称为零输入响应。

因此，总响应=强制响应+自然反应

什么是初始条件？

在一个电感器，通过它不能瞬间改变电流。这意味着通过瞬间通过电感的电流 $t = 0 ^ -$ 在瞬间过渡后将继续保持相同 $t = 0 ^ +$ ．也就是说,

$\{对齐*}我开始(0 ^ -)= I_0 = 0 =我(0 ^ +)\{对齐*}$

就电容而言，电容两端的电压不能瞬间改变。这意味着电容瞬间的电压 $t = 0 ^ -$ 在瞬间过渡后将保持不变 $t = 0 ^ +$ ．也就是说,

$\{对齐*}开始V_C (0 ^ -) = V_0 = V = V_C(0 ^ +) \{对齐*}$

驱动系列RC电路的强制响应

让我们假设电容器最初完全放电，并且切换（k）保持打开很长时间，并且它闭合 $t = 0$ ．

在 $t = 0 ^ -$ Switch K是开放的

这是一个初始条件，因此我们可以写，

(1） $\ begin {arequation *} v_c（0 ^ - ）= v_0 = v = v =c（0 ^ +）\ end {arequation *}$

因为电容器两端的电压不能瞬间改变。

对所有 $t \ geq0$ K开关闭合。

现在在电路中引入了电压源。因此，将KVL应用于电路，我们得到，

$开始\{对齐*}- r (t) - - - V_c (t) + V_s = 0 \{对齐*}结束$

（2) $\ begin {公式*} r i（t）+ v_c（t）= v_s \ end {equation *}$

现在，I（t）是通过电容器的电流，它可以以电容器跨电容器的电压表示

$\ begin {aligne *} i（t）= i_c（t）= c \ frac {dv_c（t）} {dt} \ neg {alight *}$

代入方程(2)得到，

$\{对齐*}开始RC \压裂{dV_c (t)} {dt} + V_c结束(t) = V_s \{对齐*}$

$\{对齐*}开始RC \压裂{dV_c (t)} {dt} = V_s - V_c结束(t) \{对齐*}$

分离变量，我们得到

$\ begin {aligne *} \ frac {dv_c（t）} {[v_s - v_c（t）]} = \ frac {1} {rc} dt \ neg {alight *}$

对两边积分

${对齐*}\ int \ \开始压裂{dV_c (t)} {[V_s - V_c (t)]} = \ int \压裂{1}{RC} dt \{对齐*}结束$

（3) $\{方程*}开始ln (V_s V_c (t)) = \压裂{t} {RC} + K ^ '结束\{方程*}$

在哪里 $k ^'$ 是任意常数

找到 $K'$ ：使用初始条件即，将公式（1）替换为等式（3），我们得到，

$\{对齐*}开始ln (V_s - 0) = \压裂{0}{RC} + K ^ '结束\{对齐*}$

（4) $\{方程*}{K开始^ '}= ln (V_s)结束\{方程*}$

等式（3）中的k'替换值，

$\ begin {align *} -ln [v_s - v_c（t）] = \ frac {t} {rc} - ln [v_s] \ neg {alight *}$

$\{对齐*}开始ln (V_s V_c (t)) + ln (V_s) = \压裂{t} {RC} \{对齐*}结束$

$\ begin {aligne *} ln [v_s - v_c（t）] - ln [v_s] = - \ frac {t} {rc}（[ln [a] - ln [b] = ln \ frac {a} {b}]）\结束{align *}$

$\{对齐*}开始ln \压裂{V_s - V_c (t)} {V_s} = -结束\压裂{t} {RC} \{对齐*}$

取反律，我们得到，

${对齐*}\ \开始压裂{V_s - V_c (t)} {V_s} = e ^{- \压裂{t} {RC}}{对齐*}\结束$

$\ begin {align *} v_s - v_c（t）= v_s e ^ { - \ frac {t} {rc}} \ neg {align *}$

$\ begin {align *} v_c（t）= v_s - v_s e ^ { - \ frac {t} {rc}} \ end {align *}$

（5） $\ begin {arearation *} v_c（t）= v_s（1 - e ^ { - \ frac { - t} {rc}}）v \ neg {arequation *}$

上述等式表示串联R-C电路的一阶微分方程的解决方案。

上面的响应是组合的稳态响应即。 $V_S$

和瞬态反应即， $v_s * e ^ { - \ frac {t} {rc}}$

无源串联RC电路的自然响应

无源响应是电容通过与之串联的电阻放电。

对所有 $^ + t > = 0$ 开关k关闭

将KVL应用于上述电路，我们得到，

$\ begin {aligne *} -r i（t） - v_c（t）= 0 \结束{align *}$

(6） $\ begin {arearation *} r i（t）= - v_c（t）\ end {等式*}$

$\ begin {aligal *} \，\，现在\，\，i（t）= i_c（t）= c \ frac {dv_c（t）} {dt} \ neg {alight *}$

将电流的这个值代入方程(6)，有:

$\ begin {aligne *} r c \ frac {dv_c（t）} {dt} = - v_c（t）\结束{align *}$

分离变量，我们得到

${对齐*}\ \开始压裂{dV_c (t)} {V_c (t)} = - \压裂{1}{R C} dt \{对齐*}结束$

对两边积分

$\ begin {align *} \ int \ frac {dv_c（t）} {v_c（t）} = \ int - \ frac {1} {r c} dt \ neg {align *}$

（7) $\{方程*}开始ln ({V_c (t)}] = - \压裂{1}{R C} + K ^ '结束\{方程*}$

在哪里 $k ^'$ 是任意的常数

找到 $k ^'$ :利用初始条件，即将式(1)代入式(7)，有:

$\{对齐*}开始ln (V_0) = - \压裂{0}{RC} + K ^ '结束\{对齐*}$

（8） $\ begin {arequation *} {k ^'} = ln [v_0] \ end {arearation *}$

替代价值 $k ^'$ 在等式（7）中我们得到了，

$\ begin {align *} ln [v_c（t）] = - \ frac {t} {rc} + ln [v_0] \结束{align *}$

$\ begin {align *} ln [v_c（t）] - ln [v_0] = - \ frac {t} {rc} \ end {align *}$

$\{对齐*}开始ln \压裂{V_c (t)} {V_0} = -结束\压裂{t} {RC} \{对齐*}$

取反律，我们得到，

$\ begin {align *} \ frac {v_c（t）} {v_0}} {v_0}} {v_0} = { - \ frac {t} {rc}} \ end {align *}$

（9） $\{方程*}开始V_c (t)} = V_0 e ^{- \压裂{t} {RC}}{方程*}\结束$

上式表示串联RC电路的自然响应。

现在，总响应=强制响应+自然响应

$\{对齐*}开始V_c (t) = V_s (1 - e ^{- \压裂{t} {RC}}) + V_0 e ^{- \压裂{t} {RC}}{对齐*}\结束$

$\ begin {aligne *} v_c（t）= v_s - v_s e ^ { - \ frac {t} {rc}} + v_0 e ^ { - \ frac {t} {rc}} \ neg {align *}$

$\ begin {align *} v_c（t）= v_s +（v_0 - v_s）e ^ { - \ frac {t} {rc}} \ neg {align *}$

在哪里， $V_S$ 为阶跃电压。

$v_0.$ 是电容器上的初始电压。

RC电路的时间常数

R-C电路的时间常数可以定义为跨越电容器的电压达到其最终稳定状态值的时间。

一个时间常数是电压上升到0.632倍稳态值所需的时间或电流衰减到0.368倍稳态值所需的时间。

R-C电路的时间常数是电阻和电容的乘积。

$\begin{align*} \tau = R C \end{align*}$

它的单位是第二个。

RC电路频率响应

用阻抗法：频率响应系统的一般方程是

$(\ \{对齐*}开始Hω)= \压裂{Y(\ω)}{X(\ω)}= \压裂{V_o_u_t} {V_i_n} \{对齐*}结束$

现在将潜在的分隔规则应用于上述电路

（10） $\ begin {arequation *} v_o_u_t = v_i_n \ frac {z_c} {z_c + r} \ neg {arequation *}$

在哪里， $Z_C.$ =电容器的阻抗

$\begin{align*} Z_c = \frac {1} {j\omega C} \end{align*}$

在等式（10）中替换它，我们得到，

$\ begin {align *} v_o_u_t = v_i_n \ frac {\ frac {1}} {{\ ommga c}} {{\ ommga c}}} \ end {align *}$

${对齐*}\ \开始压裂{V_o_u_t} {V_i_n} = \压裂{\压裂{1}{j \ωC}}{\压裂{1 + j \ωRC} {j \ωC}}{对齐*}\结束$

$\ begin {aligne *} \ frac {v_o_u_t} {v_i_n} = \ frac {1} {1 + j \ oomga r c} \ neg {align *}$

$\ begin {align *} h（\ omega）= \ frac {v_o_u_t} {v_i_n} = \ frac {1} {1 + j \ oomga r c} \ neg {align *}$

上述响应是R-C电路的复数形式的频率响应。

RC电路微分方程

RC充电电路微分方程

电容器上的电压由

（11） $\{方程*}开始V_c V (t) = V - e ^{- \压裂{t} {R C}}结束V \{方程*}$

现在通过电容器电流是给出的

$\ begin {align *} i（t）= i_c（t）= c \ frac {dv_c（t）} {dt} = c \ frac {d} {dt} [v - v e ^ {\ frac {-t} {rc}}] \结束{align *}$

$\ begin {aligne *} i（t）= c [0 - v（\ frac {-t} {rc}）e ^ {\ frac {-t} {rc}}] \ neg {align *}$

$\{对齐*}我开始C (t) = (- V(\压裂{1}{R}) e ^{\压裂{- t} {RC}}] \{对齐*}结束$

$\ begin {align *} i（t）= \ frac {v} {r} e ^ {\ frac {-t} {rc}} \ neg {align *}$

（12） $\ begin {arearation *} i（t）= \ frac {v} {r} e ^ {\ frac {-t} {\ tau}} a \ neat {公式*}$

RC放电电路微分方程

通过电容器的电压由

（13） $\ begin {arearation *} v_c（t）= v_0 e ^ { - \ frac {t} {r c}} v \ nod {arearation *}$

现在通过电容器电流是给出的

$\ begin {align *} i（t）= i_c（t）= c \ frac {dv_c（t）} {dt} = c \ frac {d} {dt} [v_0 e ^ {\ frac {-t} {rc}}] \结束{align *}$

$\ begin {align *} i（t）= c [v_0（\ frac {-t} {rc}）e ^ {\ frac {-t} {rc}} \ neg {align *}$

$\ begin {aligne *} i（t）= c [v_0（\ frac {-1} {r}）e ^ {\ frac {-t} {rc}} \ neg {align *}$

$\{对齐*}我开始(t) = - e \压裂{V_0} {R} ^{\压裂{- t} {RC}}{对齐*}\结束$

（14） $\{方程*}我开始(t) = - e \压裂{V_0} {R} ^{\压裂{- t}{\τ}}\结束{方程*}$

RC电路充电和放电

RC电路充电

该图示出了一种简单的R-C电路，其中电容器（C）与电阻器（R）串联，其通过机械开关（k）连接到DC电压源。电容器最初没有充电。当开关k关闭时，电容器将逐渐通过电阻充电，直到电容器两端的电压变得等于电源电压源。电容器板上的电荷作为Q = CV给出。

$\{对齐*}开始V_c V (t) = (1 - e ^{- \压裂{t} {R C}}) V \{对齐*}结束$

从上面的等式中，显然电容器电压是指数增长的。

在哪里，

$V_C$ 电容上的电压是多少
$V$ 为电源电压。

RC是RC充电电路的时间常数。即。 $\tau = R C$

将时间t的不同值代入式(11)和式(12)，得到电容充电电压，即

$\ begin {aligne *} t = \ tau \，\，然后\，\，\，v_c（t）= v - v * e ^ - ^ 1 =（0.632）v \，\，（其中，e = 2.718）\，\，\结束{align *}$

$\开始{对齐*}t = 2 \τ\ \,然后\ \,V_c e (t) = V - V * ^ - ^ 2 = (0.8646) V \{对齐*}结束$

$开始\{对齐*}t = 4 \τ\ \,然后\ \,V_c e (t) = V - V * ^ - ^ 4 = (0.9816) V \{对齐*}结束$

$\ begin {aligne *} t = 6 \ tau \，\，然后\，\，v_c（t）= v - v * e ^ - ^ 6 =（0.9975）v \ neg {alight *}$

和电容充电电流

$\开始{对齐*}t = \τ\ \,然后\ \,我(t) = \压裂{V} {R} * e ^ - ^ 1 = \压裂{V} {R}(0.368) \ \,(在那里,e = 2.718) \ \ \最终{对齐*}$

$\ begin {aligne *} t = 2 \ tau \，\，然后\，\，i（t）= \ frac {v} {r} e ^ - ^ 2 = \ frac {v} {r}（0.1353）一个\结束{align *}$

$\ begin {align *} t = 4 \ tau \，\，然后\，\，i（t）= \ frac {v} {r} e ^ - ^ 4 = \ frac {v} {r}（0.0183）一个\结束{align *}$

$开始\{对齐*}t = 6 \τ\ \,然后\ \,我(t) = \压裂{V} {R} e ^ - ^ 6 = \压裂{V} {R}(0.0024) \结束{对齐*}$

电容器上的电压的变化 $v_c（t）$ 通过电容的电流 $我(t)$ 作为时间的函数如图所示。

因此，在R-C充电电路中，如果电容器两端的电压以指数呈现，则通过电容器的电流以相同的速率指数衰减。当电容上的电压达到稳态值时，电流会降低到零值。

RC电路放电

如果现在从电池电源电压断开完全充电电容，则充电过程中电容器中的存储能量将在其板上保持无限期，将存储在其端子上的电压保持在恒定值。

现在，如果电池被短路替换，开关关闭电容器将通过电阻器放电，现在我们有一个名为RC放电电路的电路。

$\ begin {aligne *} v_c（t）= v_0 e ^ {\ frac {-t} {rc}} v \ neg {sental *}$

从上面的等式中，显然电容器电压呈指数增加。这意味着在放电R-C电路时，电容器通过电阻器R串联排出。现在R-C充电电路和R-C放电电路的时间常数是相同的并且是

$\begin{align*} \tau = R C \end{align*}$

让我们替换等式（13）和（14）中的不同时间T值，我们得到电容器放电电压，即

$\ begin {aligne *} t = \ tau \，\，然后\，\，\，v_c（t）= v_0 * e ^ - ^ 1 = v_0（0.368）v \ nod {align *}$

$\ begin {aligne *} t = 2 \ tau \，\，然后\，\，v_c（t）= v_0 * e ^ - ^ 2 = v_0（0.1353）v \ neg {align *}$

$\开始{对齐*}t = 4 \τ\ \,然后\ \,V_c e (t) = V_0 * ^ - ^ 4 = V_0结束(0.0183)V \{对齐*}$

$\ begin {align *} t = 6 \ tau \，\，然后\，\，v_c（t）= v_0 * e ^ - ^ 6 = v_0（0.0024）v \ neg {align *}$

电容器上的电压的变化 $v_c（t）$ 作为时间的函数如图所示。

因此，在R-C放电电路中，类似地，如果电压通过电容呈指数下降，通过电容的电流以相同的速率呈指数上升。当通过电容器的电压达到零值时，电流达到稳态值。