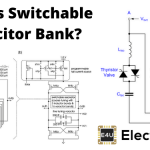
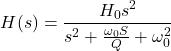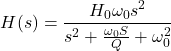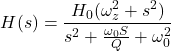Q因素:是什么?(你是怎么测量的?betway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是Q因子？

Q因子(也称为质量因子或Q因子)定义为描述欠阻尼条件的无量纲参数振荡器或谐振器。质量因子测量线圈的性能，a电容器,或者一个电感器它的损耗和谐振腔带宽。

质量因素的定义最初是由美国西部电气公司工程部的一位名叫k·s·约翰逊的工程师提出的。他测量了各种线圈的效率和一致性。在他的研究中，他发展了Q因子的概念。奇怪的是，他选择字母Q不是因为单词质量因素。因为字母表里其他的字母都被取走了。

Q因子意味着能源谐振装置内的损失，其可以是来自机械摆锤的任何东西，机械结构的实体，或来自诸如谐振电路的电路。

Q因子表示设计中所包含的能量量所造成的能量损失。因此，Q系数越大，能量损失率越低，振荡也就越慢。它们会得到较低的阻尼，而且它们的环会变长。

在电子电路中，能量损失是由电阻内部电路。虽然这可能发生在电路的某个地方，但电阻的主要触发器在电感器内部。虽然元件的Q系数对应于损耗，但它直接与谐振腔的带宽与其中心频率有关。

如何测量Q因子?

用于计算射频电路的质量因子的仪器称为Q米。Q仪表计算电路的质量因子，并表示电路消散的总能量。它还描述了线圈和电容器的特性。Q仪表用于测量线圈的射频以测量线圈的射频。

Q表的工作原理

Q计的工作原理是串联谐振。谐振是电路中电感和电容大小相等时所发生的状态。它们产生的能量在电容器和电感的电场和磁场之间振荡。q计的工作原理是基于谐振串联电路的电阻、电感和电容的特性。

正如我们所讨论的，每个Q仪表都在串联共振的原则上工作。所以，在共鸣，

$\begin{align*} X_{L} = X_{C}\end{align*}$

${对齐*}\开始E_ {L} = IX_ {L} \;\;\;\;\;E_ {C} = IX_ C {} \;\;\;\;E =红外\{对齐*}结束$

其中e是施加的电压， $E_ {C}$ 为电容器电压， $e_ {l}$ 为感应器电压， $e_ {l}$ 为感抗， $间{C}$ 为容抗，R为线圈电阻，I为电路电流。

因此，Q因子为

${对齐*}Q = \ \开始压裂{间{L}} {R} = \压裂{间{C}} {R} = \压裂{E_ {C}} {E} \{对齐*}结束$

由上式可知，如果E保持恒定，则电容两端的电压可用a来估计电压表校准直接阅读Q.

品质因数公式

谐振器的质量因子（Q）可以表征为谐振器的频率除以谐振器的带宽。

$\begin{align*}Q = frac{共振频率}{带宽}\end{align*}$

共振频率和带宽必须以相同的单位给出。

Q因子公式对于不同类型的电路是不同的。下面讨论几种不同电路的Q因子公式。

电感的Q因子

具体的无功分量的质量因数取决于它被测试的频率。这通常是包含它的电路的谐振频率。

使用包含串联损耗和完美电容的电感的谐振电路的质量因数被用来确定电感的Q因子具有串联损失阻力。给出电感的质量因子

$\{对齐*}开始Q_ {L} = \压裂{间{L}} {R_ {L}} = \压裂{\ omega_ L {0}} {R_ {L}}{对齐*}\结束$

在哪里 $\ omega_ {0}$ 是每秒弧度的共振频率，l是电感， $间的{1}$ 是感抗，和 $R_ {1}$ 为电感的串联电阻。

电容Q因数

的电容的Q系数串联损耗电阻与谐振电路的Q因数相同，谐振电路使用该电容和一个完美的电感。电容器的Q因子为

$C \{对齐*}开始Q_{} = \压裂{间{C}} {R_ {C}} = \压裂{1}{\ omega_ {0} CR_ {C}}{对齐*}\结束$

在哪里 $\ omega_ {0}$ 每秒弧度的共振频率是电容， $间{C}$ 是感抗，和 $R_ {C}$ 是电容器的串联电阻。

一般来说，谐振器的Q因子可以由元件的Q因子值来解析，谐振器由电容和电感组成。这适用于它们的损耗是由串联电阻引起的还是不同的。

$\ begin {align *} q = \ frac {1} {\ frac {1} {q_ {l}} + \ frac {1} {q_ {c}}} \ neg {senvent *}$

LC电路的Q因数

在并行LC电路中，电感的电阻R与电感l是串联的，这是LC电路的主要问题之一。但是Q和串联电路中的是一样的。因此Q因子为

$\{对齐*}开始Q = \压裂{1}{R} \√6{\压裂{L} {C}} = \压裂{\ omega_ L {0}} {R} = \压裂{1}{\ omega_ RC}{0}{对齐*}\结束$

其中调谐电路的电阻，电感和电容是R，L和C.

RLC电路的Q因子

调谐射频接收器是一类无线电接收器，其包含一个或多个调谐的射频放大器级，其伴随着解调器电路，以收集音频信号和通常是音频放大器。

理想系列的质量因素RLC电路以及调谐无线电频率接收器(TRF)的资料如下。

$\{对齐*}开始Q = \压裂{1}{R} \√6{\压裂{L} {C}} = \压裂{\ omega_ L {0}} {R} = \压裂{1}{\ omega_ RC}{0}{对齐*}\结束$

其中调谐电路的电阻、电感、电容为R、L、c。当序列电阻越大，电路中Q的值就越小。

对于并联RLC电路，采用问因子将是串联RLC电路的逆。

$\{对齐*}开始Q = R \√6{\压裂{C} {L}} \压裂{R} {\ omega_ L {0}} = \ omega_ RC \{0}{对齐*}结束$

想象一个电路，R, L和C都是平行的。并联电阻越低，对电路阻尼的影响就越大，因此q值也就越低。这在确定带宽的滤波设计中很有用。

Q因子传递函数

滤波器响应可以由S域表示传递函数。参数S来自于拉普拉斯变换并且代表复杂频率滤波器也具有质量因子Q，并且通常表示为 $\α$ 。

$\ begin {aligne *} \ alpha = \ frac {1} {q} \ neg {alight *}$

这通常称为阻尼比。 $\ xi = 2 \ alpha$ 。

Q因子低通滤波器

$\{对齐*}开始H (s) = \压裂{K}{1 + \压裂{年代}{\ omega_{0}}}{对齐*}\结束$

这个传递函数是一阶频域作用的数学解释低通滤波器。同样的传递函数可以用质量因子和表示 $\ omega_ {0}$ 也。

$\ begin {align *} h（s）= \ frac {h} {s ^ 2 + \ frac {\ oomega_0 s} {q} + \ oomega_0 ^ 2} \ end {aligh *}$

在哪里 $H_0$ 通频带增益和 $\ omega_0$ 是个截止频率。

q因子高通滤波器

将低通滤波器转换为高通滤波器，则低通滤波器传递函数的分子为 $H_0s ^ 2$ 。高通滤波器的输出以低通滤波器形式类似，但频率翻转。

$\{对齐*}开始H (s) = \压裂{H_0s ^ 2} {s ^ 2 + \压裂{\ omega_0年代}{Q} + \ omega_0 ^ 2} \{对齐*}结束$

Q因子带通滤波器

低通滤波器的分子改变为 $H_0 \ omega_0s ^ 2$ ，以取得带通滤波器函数。

$\ begin {aligne *} h（s）= \ frac {h_0 \ omega_0s ^ 2} {s ^ 2 + \ frac {\ oomega_0 s} {q} + \ \ oomega_0 ^ 2} \ neg {alight *}$

在哪里 $\ omega_0$ 为截止频率。 $H_0$ 为电路的增益。

$\begin{align*} H_0 = \frac{H}{Q}\end{align*}$

在带通滤波器设计中，Q被称为滤波器的选择性。

${对齐*}Q = \ \开始压裂{F_0} {F_H - F_L} \{对齐*}结束$

在哪里 $F_H$ 和 $F_L$ 是响应距离最大值3分贝的频率吗

Q因子缺口（BandStop）过滤器

当带通滤波器的分子变为 $s ^ 2 + \ oomega_z ^ 2$ 时，可以得到带阻滤波器(也称为陷波滤波器或带阻滤波器)。窄带阻滤波器称为陷波滤波器，宽带阻滤波器称为带阻滤波器。

带阻滤波器的传递函数为

$\{对齐*}开始H (s) = \压裂{H_0 (\ omega_z ^ 2 + s ^ 2)} {s ^ 2 + \压裂{\ omega_0年代}{Q} + \ omega_0 ^ 2} \{对齐*}结束$

Q因子与阻尼

Q因子用于确定简单阻尼振子的定性行为。在物理系统中，阻尼是由耗散储存在振荡中的能量的过程产生的。

覆盖条件：当质量因数低( $q <\ frac {1} {2}$ ）.这个系统根本不振荡。所以当它从稳态平衡输出转移时，它通过指数衰减回到相同的位置，渐近地达到稳态值。

它具有脉冲响应，即两种具有不同衰减速率的衰减指数函数的总和。具有非常低质量因子的二阶低通滤波器几乎是一阶相响应。设备的输出通过慢慢上升到渐近的渐近来响应步进输入。

受损条件：当质量因数低( $问> \压裂{1}{2}$ ）.欠阻尼系统在特定频率上的振荡与信号振幅的衰减相结合。

质量因子较差的欠阻尼系统在消失之前可能只会振荡一次或几次。如果质量分量增加，阻尼的相对数量就会减少。更广泛地说，具有非常高质量因子的二阶低通滤波器的性能指的是上面迅速增加的阶跃输入，振荡通过，并逐渐收敛到一个稳态值。

严重阻尼条件：当质量因数是中间的时，据说一个系统批判性地阻尼（ $Q = \压裂{1}{2}$ ）.作为过度阻尼系统，输出没有真正振荡，因此不会过度过冲其稳态输出。

与欠阻尼系统一样，该系统的输出对单位阶跃输入响应迅速。临界阻尼的结果是不超调的最终值的最佳答案。

共同系统的质量因素

临界阻尼系统的一个很好的例子是单位增益萨伦基低通滤波器拓扑。它有相同数量的电容器和电阻。所以质量因素是 $Q = \压裂{1}{2}$

欠阻尼条件的一个例子是二阶巴特沃斯滤波器。质量因素是 $Q = \压裂{1}{\ sqrt {2}}$

Q因子的影响

有几个原因，为什么Q因素是重要的工作时，射频调谐电路。通常，高级别的Q因子是有利的，但有些实现可能需要给定级别的Q因子。下面总结了射频调谐电路中与Q因子相关的一些问题。

带宽:

如果质量因子增加，调谐电路滤波器的带宽就会减少。随着损耗的减少，调谐电路变得更加尖锐，因为能量最好地保留在电路中。可以看出，随着Q因子的增加，3db的带宽减小，调谐电路的总输出增加。在某些情况下，高Q因子是必要的，以确保实现相关的选择性程度。

因此，在许多应用中，必须计算所需的Q因子的量，以便提供满足广泛带宽标准所需的总输出和可接受的不希望信号的可接受拒绝。

振荡器相位噪声：

任何振荡器都可以产生相位噪声。这涉及信号过程中的随机变化。这表现为从主要载体延伸出的破坏。预期，不需要这种噪音，因此需要减少。

响了:

如果谐振电路的Q系数增大，则损耗减小。这就确保了电路内部的任何振荡都需要更长的时间才能停止。换句话说，电路看起来更“响”。事实上，这适合在振荡器电路中使用，因为它更容易建立和维持振荡，因为在调谐电路中浪费的能量更少。