八进制数系

在早期八进制数系大多用于小型计算机。“OCT”这个词意味着八个。八进制数系表明它是基础8的数字系统，这意味着我们需要8个不同的符号，以表示八进制系统中的任何数量。符号为0,1,2,3,4,5,6和7.该系统中最小的两位数字为（10）_8.这相当于十进制8。
例如，在此数字系统中，该数字写为（352）_8.。基础应写入为8，否则将默认假定数字以十进制数系统。所以需要处理编写数字。一点点错误可能导致数字系统基础的变化。使用八进制数系的主要优点是它可以以非常简单的方式直接转换为二进制。正如我们所知，计算机只懂二进制数字系统因此，从二进制到八进制或八进制到二进制的转换更容易，因此使用该数字系统。

因为它的基础是8 = 2^3.，该系统的每个符号都可以由其三位二进制等效表示。

由于八进制系统中的每一位数字都分别用其3位二进制等量表示，所以八进制系统需要的长度是二进制数的三分之一。它基本上是一个位置加权的数字系统。八进制中数字位置的权值为

数字转换

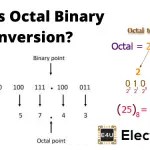
八进制到二进制转换

转换是通过将单个八进制数字转换为二进制来完成的。每个数字必须转换为3位二进制数，结果将是八进制数的二进制等效物。

例子
转换（145.56）_8.二进制 -

该表应使用，以便将任何八进制数转换为二进制文件。从表格中，写出我们获得的每个数字的二进制等同物 -

这是八进制数的二进制等同物。

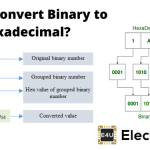
二进制到八进制的转换

可以使用相同的表，以便将二进制数转换为八进制。首先，将二进制数组分组为三位组，并写出它的八进制等价物。

例子
八进制等价物（11001111）₂是
我们来到这里的团体是 -
011,001,111。添加号码之前的零，以便以三位二进制数字的形式完成分组。

这两个数的八进制等号是-
3,1，7.因此我们得到的八进制数是（317）_8.。

八进制十进制转换

将八进制数转换为十进制等价物的方法非常简单。只需将八个基数的数量展开，其位置重量，结果将是十进制数。

例子
转换（317）_8.到了十进制等价物。
这可以如下完成 -

十进制到八平化转换

这可以通过使用称为双达贝法的重复分割方法将数量除以8来完成。重复的分裂是完成的，剩余的是。它可以如下完成 -

例子
求等于158的八进制数。

八进制系统中的等效数是（236）_8.。
当分数或小数点之后有一个数字时，可以转换为 -
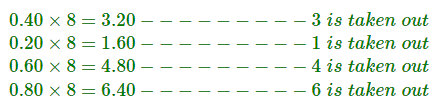
说我们必须将0.40转换为八进制。

所以我们看到数字重复。这将继续下去，它将是一个永无止境的过程，所以我们可以近似结果 -
(.3146…)_8.。

八进制数系的优点

1. 它是二进制的三分之一。
2. 简单的转换过程，从二进制到八进制，反之亦然。
3. 更轻松地以八进制形式处理输入和输出。

八进制数系的缺点

电脑不明白八进制数系因此，在将其应用于数字系统或计算机之前，必须有一个已知的附加电路作为二进制转换器。