诺顿定理:它是什么?诺顿等效电路(Norton Equivalent Circuitbetway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是诺顿定理？（诺顿的等效电路）

Norton的定理（也称为Mayer-Norton定理），可以将任何线性电路简化为具有连接到负载的单电流源和等效的并联电阻的等效电路。简化电路称为Norton等效电路。

更正式地，诺顿的定理可以说：

“具有任何线性双侧元素和有源源的电路可以由由阻抗和a组成的简单的双终端网络代替当前的来源，不管网络的复杂性。”

诺顿定理平行于戴维宁定理。它广泛用于电路分析，以简化复杂的网络，并研究电路的初始条件和稳态响应。

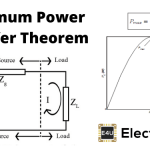
如上图所示，任何复杂的双边网络都简化为简单的Norton等效电路。

Norton等效电路包括相同的电路阻抗与电流源和负载平行连接抵抗性。

Norton等效电路中使用的恒流源称为Norton Current i_N.或短路电流i_SC.。

诺顿定理是由汉斯费迪南德市长和爱德华·劳瑞诺顿于1926年得出的。

Norton等效公式

如Norton等效电路所示，Norton电流分为两条路径。一条路径通过等效电阻，第二路径通过负载电阻。

因此，通过负载电阻的电流可以由当前分频器规则导出。诺顿定理的公式是;

$\ [i_l = \ frac {r_l {eq}} {r_l + r_ {eq}} \ times i_n \]$

如何找到Norton等效电路

任何复杂的双边网络都被简单的Norton等效电路所取代。它包括;

诺顿等效电阻
Norton等效电流
负载阻力

Norton等效阻力

Norton等效电阻类似于临时等效电阻。要计算Norton等效电阻，我们需要删除网络的所有活动源。

但条件是;所有来源必须是独立的来源。如果网络由依赖源/秒组成，则需要使用其他方法来查找Norton等效电阻。

如果，网络仅由独立源组成，通过短路从网络中删除所有来源电压电源和开路电流源。

在计算Norton等效电阻的同时，负载电阻是开放式的。并找到开路电压在负载端子之间。

有时，Norton电阻也称为紫外线等于的电阻或开路电阻。

让我们用一个例子来理解。

首先，检查具有任何依赖源的网络吗？在这种情况下，所有来源都是独立的来源;20V电压源和10A电流源。

现在，通过短路电压源和开路电流源取出两个源。打开负载终端。因此，网络仍然如下图。

现在，通过制造串联和平行电阻来找到开路电压。

电阻6Ω和4Ω串联。因此，总电阻为10Ω。

两个10Ω电阻并联。所以，等效电阻r_eq.=5Ω。

诺顿等效电流

为了计算Norton等效电流，负载电阻短路。并找到通过短路分支的电流。

因此，Norton电流或Norton等效电流也称为短路电流。

在上面的示例中，拆下负载电阻并使负载分支短路。

在上述网络中，包含电压源的分支由于它是冗余分支而被忽略。这意味着它是短路分支的并行分支。

$\ [i_1 = 10a \]$

在Loop-2中应用KVL;

$\ [10i_2 - 6i_1 = 0 \]$

$\ [10i_2 - 60 = 0 \]$

$\ [10i_2 = 60 \]$

$\ [i_2 = i_ {n} = 6a \]$

因此，Norton等效电路如下图所示。

通过负载的电流为I_L.。根据这一点当前的分隔规则;

$\ [I_L = \压裂{R_ {EQ}} {R_ {EQ} + R_L} \ * I_ {N} \]$

$\ [i_l = \ frac {5} {5 + 5} \ times 6 \]$

$\ [i_l = 3a \]$

诺顿等效电阻与依赖源

为了计算具有依赖源的电路的Norton等效电阻，我们需要计算开路电压（V._OC）跨越负载终端。

开路电压类似于临时等效电压。

在找到母线等效电压和诺顿电流后;将此值放在以下等式中。

$\ [R_ {EQ} = R_N = \压裂{V_ {TH}} {I_N} = \压裂{V_ {OC}} {I_ {SC}} \]$

Norton等效电路示例

示例1在终端AB上找到Norton等效电路。

在给定的主动线性网络中查找跨终端AB的Norton等效电路，如下图所示。

步骤1求诺顿等效电流(I_N.）。计算I._N.，我们需要短路终端AB。

在Loop-1中应用KVL;

（1） $\ begin {arequation *} 60 = 10i_1 - 5i_2 \ end {公式*}$

在Loop-2中应用KVL;

$\ [0 = 40i_2 - 5i_1 - 20i_3 \]$

来自电流源;

$i_3 = 2a$

因此;

$\ [0 = 40i_2 - 5i_1 - 20（2）\]$

（2） $\ begin {arearation *} 40 = -5i_1 + 40i_2 \ end {等式*}$

通过求解公式-1和2;我们可以找到当前I的价值₂与诺顿电流相同（我_N.）。

$\ [i_2 = i_n = 4a \]$

第2步找到相同的阻力（r_eq.）。为此，电流源打开循环和电压源短路。

$\ [5 || 5 = 2.5 \ omega \]$

$\ [20 + 15 + 2.5 = 37.5 \ omega \]$

步骤3.在Norton等效电路中置于Norton电流和等效电阻的值。

示例2找到给定网络的Norton和母线等效电路

步骤1找到Norton Current（I_N.）。对于那个短终端AB。

将KVL应用于环路1;

$\ [20 + 4i = 14i_1 - 6i_2 \]$

$\ [i = i_1 - i_2 \]$

$\ [20 + 4（i_1 - i_2）= 14i_1 - 6i_2 \]$

$\ [20 + 4i_1 - 4i_2 = 14i_1 - 6i_2 \]$

（3） $\ begin {arequation *} 20 = 10i_1 - 2i_2 \ end {公式*}$

现在，在Loop-2处应用KVL;

$\ [18i_2 - 6i_1 = 0 \]$

$\ [6i_1 = 18i_2 \]$

$\ [i_1 = 3i_2 \]$

将此值放在公式-3中;

$\ [20 = 10（3i_2） - 2i_2 \]$

$\ [20 = 28i_2 \]$

$\ [i_2 = i_n = 0.7142 a \]$

第2步网络由依赖电压源组成。因此，等效阻力无法直接找到。

为了找到等效电阻，我们需要找到开路电压(戴维宁电压)。对于开路端子AB，由于开路，流过12Ω电阻的电流为零。

所以，我们可以忽略12Ω滤压。

$\ [20 + 4i = 14i \]$

$i = 2A$

6Ω电阻上的电压与端子AB上的电压相同。

$\ [v_ {oc} = v_ {th} = 6 \ times 2 \]$

$\ [v_ {th} = 12v \]$

步骤3.找到等效电阻;

$\ [r_ {eq} = \ frac {v_ {th}} {i_n} \]$

$\ [r_ {eq} = \ frac {12} {0.714} \]$

$\ [r_ {eq} = 16.8 \ omega \]$

第四步在Norton等效电路中置于Norton电流和等效电阻的值。

步骤5.将紫色电压和等效电阻的值置于临时等效电路中的价值。

Norton和临时等同电路

Norton等效电路是一个双网络临时等效电路。诺顿和紫素本定理广泛用于在网络分析中解决复杂电路。

如我们所见，Norton等效电路由Norton电流源组成，并且临时等效电路由临时电压源组成。

两种情况下等效电阻是相同的。将诺顿转换为临时等效电路，源转换用来。

在上述示例中，可以将Norton电流源和并联等效电阻转换为串联连接的电压源和电阻。

电压源的值将是;

$\ [v_ {th} = \ frac {i_n} {r_ {eq}} \]$

你会得到精确的母线等效电路。