网络分析是一个可以计算a的不同电参数的过程吗电路元件连接在一个电网络．一个电路或网络也可以复杂，在复杂的网络中，我们必须应用不同的方法来简化网络以确定电气参数。这电路元件在网络中可以以不同的方式连接，其中一些是并行地串联和一些。这电路元件是电阻那电容器那电感器那电压源那目前的来源等。当前的那电压那电阻、阻抗、电抗电感那电容,频率,电力那电能等等是我们所确定的不同的电参数网络分析．简而言之，我们可以说电网络是组合不同的电路元件和网络分析还是电路分析是确定这些不同电气参数的技术电路元件．
电力网图
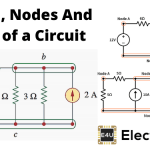
当我们用手绘线代替电网中的所有电路元件时，这个图形就被称为电路图网络图．下面的图- 2显示图上述网络在图- 1中。
该线表示电路元件称为网络的分支。两个或多个分支机构的点称为网络的节点。通过元素的电流方向由在分支上绘制的箭头表示。图表中的电流的方向可以任意地考虑。当我们在每个分支中绘制具有电流方向（方向可能是任意的）的网络图时，将调用图表有向图网络。下面的图3显示了有向图上述网络在图- 1中。
当一个主动网络被表示为一个被动网络时，通过一个图去掉电压和电流源那么图表被称为面向拓扑图网络。这电压源通过用短路替换它来消除，用开路替换电流源来消除。
上面的图 - 4显示了一个带有两者的电气网络电压源和电流源。下面的图- 5显示面向拓扑图图中的网络 - 4。
网络分析术语的定义
分支
在图形中的每条手绘制的线，表示流动电流的路径称为分支。
节点
其他分支机构的分支的终点被称为节点。
子图
这是一个图的分支的子集。
树
树是一个子图，它包含了图的所有节点，但没有形成任何闭合回路。如果图中有n个节点，则树将有(n - 1)个分支。树的枝条被称为细枝。因此，一棵树也可以被称为一组树枝。
CoTree
余树是一个子图，它包含树中不包含的所有分支。cotree是树的互补。
等效电路
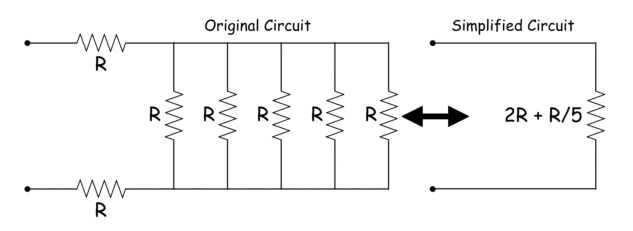
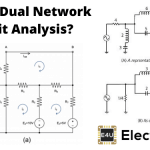
网络分析的主要步骤是将比较复杂的网络简化为其简化形式。通常可以将阻抗串联和并联来实现。有时需要将网络的部分或全部电压源转换为电流源，反之亦然。如果我们考虑有源网络的任意两个终端，很明显，两个终端之间会有电压和电流。对网络进行简化后，通过这两个终端，两端的电压和电流保持不变。虽然网络结构已经发生了重大变化。原始电路(或网络)和简化电路(或网络)称为相互等价的电路。在无源网络的情况下，在简化网络后，跨越网络任意两个参考端的阻抗保持相同。
串并联电路
在网络分析中，最常做的活动是组合串联和并联电路元件。
如果是的电阻是串联的时，等效电阻的值为:
如果是的电阻并联时，等效电阻的值为:
如果是的电感串联连接，则等效电感值为:
如果是的电感是并联的，则等效电感值为:
如果是的电容串联连接，则等效电容值为:
如果是的电容并联连接，则等效电容值为:
如果n个阻抗串联，则等效阻抗为:
如果n个阻抗并行连接，则相同阻抗的值将是，
星三角洲转型
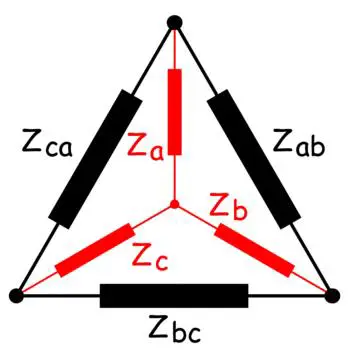
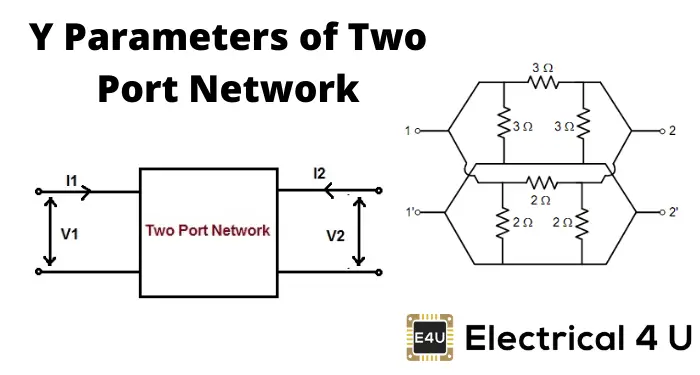
在双端网络中，端口间的阻抗可以很容易地用阻抗的串并联组合来简化。如果一个网络的终端数超过两个，那么终端之间的等效阻抗可能不能通过简单的阻抗串联和并联组合来求解。让我们考虑三端网络。端口之间的阻抗或任何其他类似的参数要么是星形连接，要么是三角形连接。这δ连接网络可以转换成星连接网络反之亦然。在网络分析期间，我们必须转换为*或者*转换为简化网络。让我们考虑一个由三个阻抗Z组成的三端网络一种, ZB., ZC连接在明星。考虑另一个由三个阻抗Z组成的三个终端网络ab, Z公元前, Z加利福尼亚州．如果这两个网络是等价的，那么星和的阻抗之间的关系是这样的。
电源转换
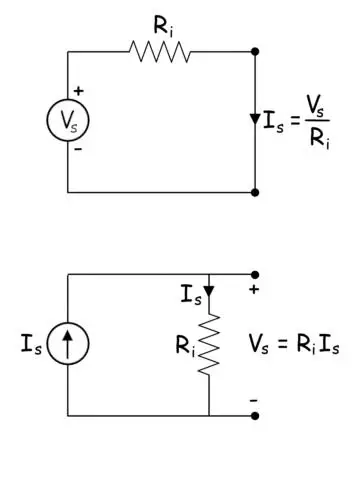
在网络分析中经常使用的另一个关键步骤是源转换．为了简化复杂的电路，常常必须把电流源转换为电压源，把电压源转换为电流源电网络．在现实中一个实用电压源可以被认为是理想电压源与内阻串联。同样，一个实际的电流源可以看作是一个理想的电流源，它的内阻是并联的。当电压源与电路连接时，它在电路的两端施加电压，并根据电路的阻抗和电源的串联内阻为电路提供一定的电流。当电流源在连接到相同的两端时向电路提供相同的电流时，电流源可以说是等效的电压源。发现电流源的电流为电压源的短路电流，内阻与电压源的内阻相同，只是并联而不是串联。这意味着如果我们短路一个电压源的两个端点，流过该设备的电流是等效电流源的电流。类似地，当一个电流源是开路时，电源开路端出现的电压将是等效电压源的电压。
电压分流规则
通常使用的网络分析技术是电压和电流划分规则．电压划分规则计算电压源上一系列阻抗中某一特定阻抗上电压降的过程。假设有n个阻抗Z1, Z2, Z3....... ..N串联在电压V的电压源上S.．然后是阻抗Z上的电压降1是，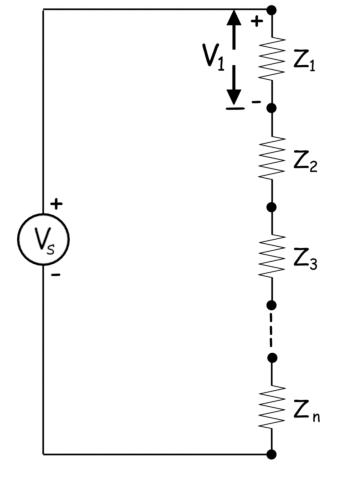
在上图中，我们将阻抗视为电阻，但根据电路的要求，我们可以考虑任何其他阻抗参数而不是电阻。
同样，跨越任何特定阻抗Z的电压降一世是（谁）给的
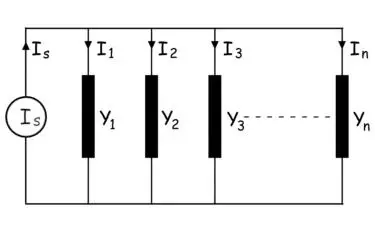
我们取电流I的一个电流源S.通过n个并行连接导纳y1Y2Y3.Y……N．
电流通过导纳y1表示为
类似地，电流通过导纳y一世是，
节点分析和网格分析
网络分析中使用了其他两个重要方法。这些是节点分析和网眼分析。这是不用的，说这两种方法是最常见的，最常用于网络分析。这两种方法是节点分析和网孔分析法．网络的节点分析主要涉及基尔霍夫电流定律也就是说，进入节点的电流等于离开节点的电流。换句话说，所有进入和离开结点的电流之和等于零。如果一个节点(网络分支的连接点)有n个分支，I1,我2,我3.….. 一世N是通过各自分支的电流，
网格是网络的循环，其不包含内部的任何其他循环。网络网格的边缘由网络的分支形成。按照网孔分析法，跨越每个分支的电压之和为零。这意味着沿着网格的边缘在任何特定方向上，电压增益的总总数与电压降的总数恰好等于电压下降。这只是Kirchhoff的电压法．如果n个分支形成网格，并且相应分支的电压是v1, V2, V3.VN然后我们可以写，
叠加定理
在网络分析中另一种流行的电路求解方法是叠加定理．该方法适用于具有多于一个电源的活动网络。在叠加技术中，除了一个之外，我们首先必须通过其内部阻抗删除所有来源。首先计算该特定源对网络的分支的影响。这意味着在网络中的连接源计算该分支的电压或电流或两个。然后我们删除源将其内部阻抗保持在地点并重新连接到网络中的第二个来源。现在我们必须计算相同分支的所需参数。通过这种方式，我们必须逐一重新连接并删除所有来源并每次计算所需的参数。最后通过对分支机构上的所有单个源的符号进行求和，我们在所有源连接到网络时获得对分支的累积效果。
诺顿定理
的概念诺顿定理非常简单。考虑任意分支电网络．如果网络处于活动状态，则必须有一定的电流流过分支。电流的起源是有源网络本身，并且流过BRACH的电流量是由于网络的等同阻抗和分支本身的阻抗。随着网络的其余部分提供电流向分支提供电流，如果分支是短路的并且具有与源相连的网络的等效阻抗，则网络可以被认为是当前电流的理想电流源。简化了向等效电流源简化了网络的过程爱德华·劳瑞诺顿被称为诺顿定理．
母亲定理
的概念母亲定理类似于诺顿定理，但这里整个活动网络被认为是一个电压源穿过分支。源的电压是跨越分支的网络的开路电压，串联连接的源的阻抗是网络跨越分支的等效阻抗。将活动网络简化为单个的过程电压源是由利昂·查尔斯·戴维南．
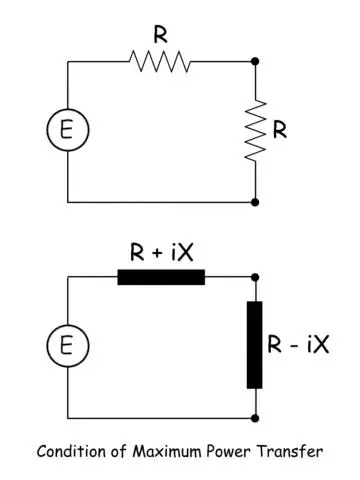
最大功率传递定理
在电阻有功网络中，当网络两端的等效电阻与两端相连支路的等效电阻完全相等时，最大功率就从网络转移到电阻支路。没有完全电阻的网络最大功率传递定理可以在下面的语句中定义。在有源网络中，当两个终端之间的网络等效阻抗是两个终端之间的支路阻抗的复共轭时，最大功率将从网络转移到支路。
