米尔曼定理

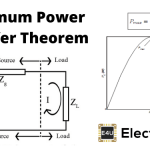
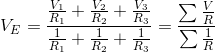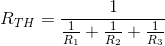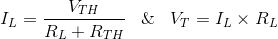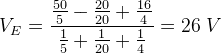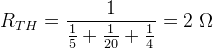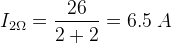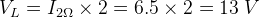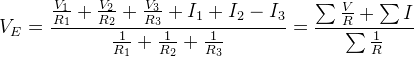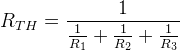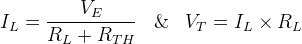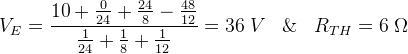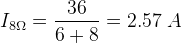米尔曼定理以提出该定理的著名电气工程教授雅各布·米尔曼的必威电竞赞助名字命名。米尔曼定理在简化特殊类型的复形时是一个非常有力的工具电路．这个定理不过是戴维宁定理和诺顿定理．这是一个非常有用的定理电压通过负载和当前的通过负载。This theorem is also called as平行发电机定理．
米尔曼定理适用于可能只包含电压源在并联或混合电压和电流源并行连接。让我们逐一讨论这些问题。

仅包含电压源的电路

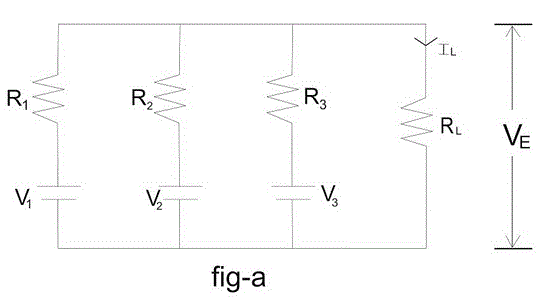
我们有一个如下图a所示的电路。

这里V₁, V₂和V_3.电压分别是1吗^圣， 2^nd和3^{理查德·道金斯}分支和R₁, R₂和R_3.是他们各自的阻力。我_l, R_l和V_T是负载电流，负载电阻和终端电压分别。
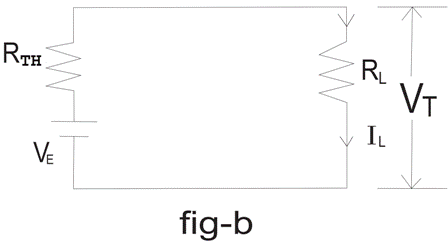
现在，这个复杂的电路可以很容易地减少到一个等效电压源的串联电阻借助于米尔曼定理如图B所示。

等效电压V的值_E根据Millman的定理指定了 -

这个V_E除了达维宁电压和达维宁电阻R什么都不是_TH可以通过短路源根据惯例来确定。所以R._TH将以

现在负载电流和终端电压可以很容易地通过

让我们通过一个例子来理解米尔曼定理的整个概念。

例子- 1
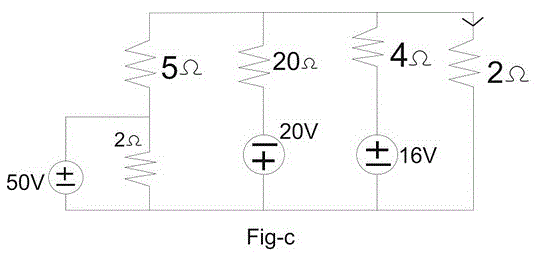
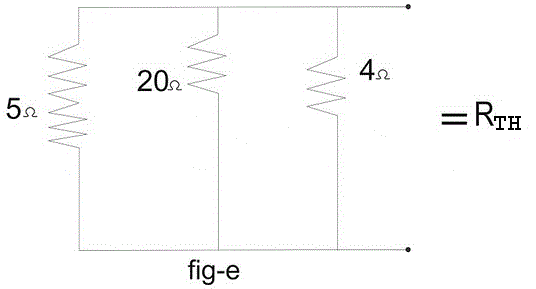
电路如图-c所示。找出2欧姆电阻上的电压和通过2欧姆电阻的电流。

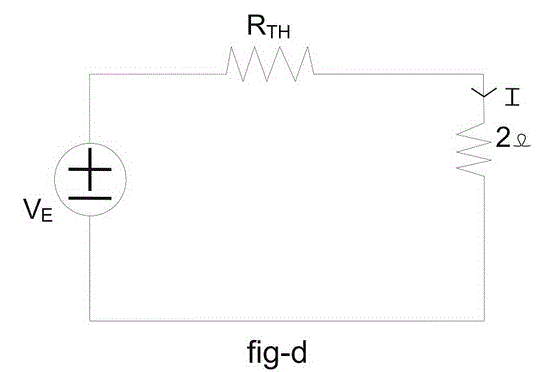
答:我们可以通过任何解决方法来解决这个问题，但最有效和节省时间的方法将不是另外一个米尔曼定理．给定电路可简化为图-d中所示的等效电压V的电路_E可以通过密尔曼定理得到，那是


如图e所示，通过短路电压源可以得到等效电阻或泰韦宁电阻。


现在我们可以很容易地找到通过2欧姆负载所需的电流电阻通过欧姆定律．

跨负载电压为，

电路为电压和电流混合电源

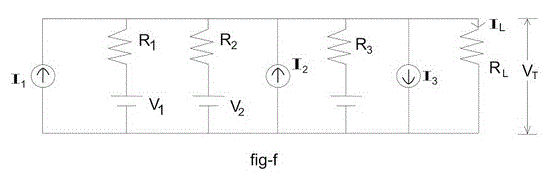
米尔曼定理还有助于减少与单个等效电压或电流源并联连接的电压和电流源的混合。让我们有一个如下图所示的电路 - f。

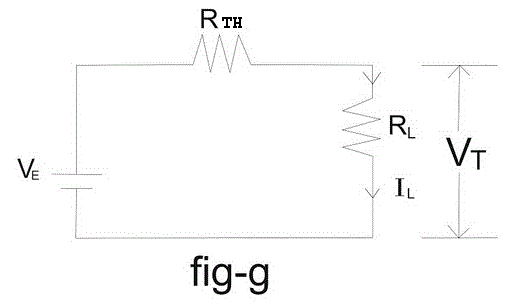
这里所有的字母都表示它们的传统表示。这个电路可以简化成图- g所示的电路。

这里V_E也就是根据米尔曼定理得到的维宁电压也就是根据米尔曼定理得到的维宁电压

和R_TH用开路代替电流源，用短路代替电压源。

现在我们可以很容易地求出负载电流I_l和终端电压V_T欧姆定律。

让我们通过一个例子来更正确地理解这个概念。

示例2:

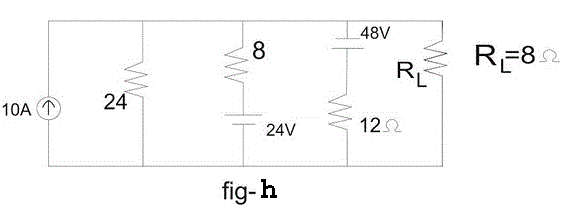
电路如图h所示。求通过负载电阻的电流R_l= 8Ω。

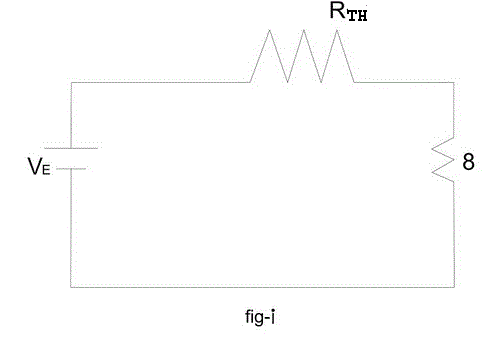
答:这个问题似乎很难解决，而且很耗时，但在帮助下，它可以很容易地在很短的时间内解决米尔曼定理．给定的电路可以用图- i所示的电路进行简化，其中V_E借助米尔曼定理，


因此，电流通过负载电阻8Ω是，