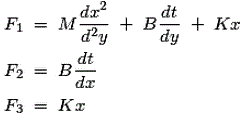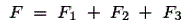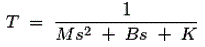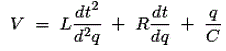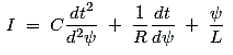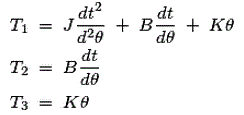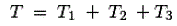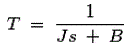控制系统的数学建模
有各种类型的物理系统,即我们有:
- 机械系统
- 电气系统
- 电子系统
- 热系统
- 液压系统
- 化学系统
首先我们需要了解 - 为什么我们需要首先建模这些系统?控制系统的数学建模是为这些类型的系统绘制框图的过程,以便确定它们的性能和传输功能。
现在让我们详细描述系统的机械和电气类型。我们将在理解控制系统理论方面源于机械和电气系统之间的类比。
机械系统的数学建模
我们有两种机械系统。机械系统可以是线性机械系统也可以是旋转机械系统。
在线性机械系统中,我们有三个变量:
- 力,用F表示
- 速度,由'v'表示
- 线性位移,由'x'表示
我们还有三个参数:
- 质量,由'm'代表
- 粘性摩擦系数,用“B”表示
- 弹簧常数,用K表示
在旋转机械类型的系统中我们有三个变量:
- 扭矩,由't'表示
- 角速度,用' ω '表示
- 角位移,由'θ'表示
我们还有两个参数:
- 惯性矩,由'j'表示
- 粘性摩擦系数,用“B”表示
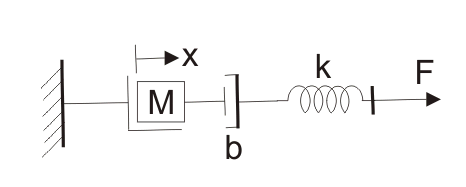
现在让我们考虑下面显示的线性位移机械系统 -
我们已经在图表本身中标记了各种变量。我们有x是如图所示的位移。从牛顿的第二次议案法中,我们可以写作力量 -
从下面的图表中,我们可以看到:
取代f的值1F2和F3.在上面的等式和服用的拉普拉斯变换我们有转移函数,
这个等式是机械控制系统的数学建模。
电气系统的数学建模
在电气类型的系统中我们有三个变量-
- 用V表示的电压。
- 电流,用“I”表示。
- 用'q'表示的电荷。
而且我们还有三个参数主动和被动组件:
- 电阻由'r'表示。
- 由'C'表示的电容。
- 电感,用“L”表示。
现在我们处于条件方面,可以在电气和机械类型的系统之间获得类比。有两种类型的类比,它们写下来:
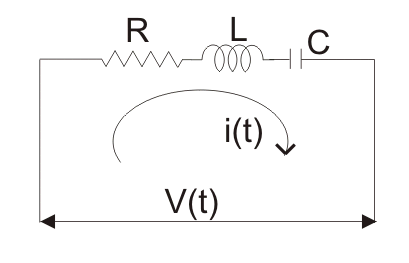
力电压类比:为了理解这种类比,让我们考虑一个由串联组合组成的电路电阻器那电感器和电容器。
一种电压如电路图所示,V与这些元件串联。现在从电路图和帮助下kvl.方程式我们在充电方面写下电压的表达,抵抗性那电容器和电感,
现在将上面与我们派对的机械系统进行比较,我们发现了 -
- 质量(m)类似于电感(左)。
- 力类似于电压V.
- 位移(x)类似于电荷(Q)。
- 摩擦系数(B)类似于阻力R和
- 弹簧常数类似于电容器(C)的倒数。
这种类比被称为力电压类比。
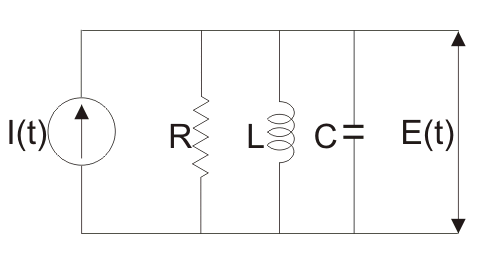
强制电流比喻:为了理解这种类比,让我们考虑一个由电阻,电感器和电感器和的并联组合组成的电路电容器。
电压E与这些元件并联连接,如电路图所示。现在从电路图和帮助下氯化钾我们把电流的表达式写成通量,电阻,电容器和电感器作为,
现在将上面与我们派生的机械系统相比,我们发现了这一点,
- 质量(M)类似于电容器(C)。
- 力类似于电流I。
- 位移(x)类似于通量(ψ)。
- 摩擦系数(B)类似于抵抗性1 / r和
- 弹簧常数K类似于电感器(L)的倒数。
这种类比被称为力电流类比。
现在让我们考虑如下所示的旋转机械类型,我们已经在图中标记了图中的各种变量。我们具有θ是角位移,如图所示。从机械系统中,我们可以为扭矩(类似于力)的方程写入扭矩,如扭矩
从图中我们可以看到,
取代t的值1T2和T3.在上面的等式和服用的拉普拉斯变换我们有转移函数,
这个方程是数学建模电气控制系统。