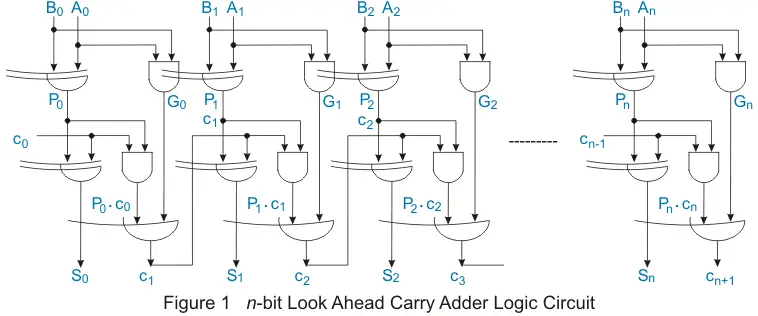
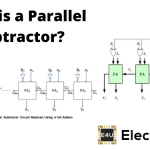
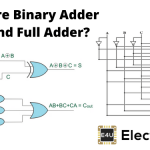
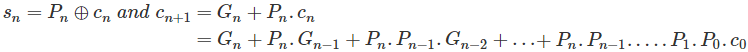我们已经看到，使用全加法器的级联安排构建的并行加法器电路高度受与进位位传播相关的延迟的影响(在文章中有更多这方面的内容)。并行加法器”)。需要添加的比特数越大，相关的延迟就越大。如果我们需要摆脱这种“延迟”问题，那么我们就需要进行设计超前进位加法器电路．
超前进位加法器的工作原理
为了克服纹波进位传播延迟，一种解决方案是提前很好地预测可能导致进位位元产生的情况。越早做越好。因此，如果我们能通过观察需要加的输入位来确定是否得到进位，那将是最好的。
现在假设我们有输入位相加为0和0或1和0或0和1，那么和就是0或1或1，没有进位。另一方面，如果两个输入位都是1，那么和就是1，就会产生进位。需要注意的是，这些陈述只有在携带(c我)位，该位需要与输入位相加为零。现在我们假设这个c我是1。在这种情况下，所有情况(0和1的组合，1和0和1和1的组合)都会产生进位，除非两个输入位都是0。
结合这两个因素，可以得出结论，我们将得到进位项
在两种情况下:(i)当两个输入位(a我b我)为1或(ii)时，任何输入位(a我b我)为1，其进位是将前面的输入位(c我)是1。
这些语句可以用逻辑表达式等价表示为
进位的表达式合起来可以写成
然而，我们有和的逻辑表达式保持这样。
接下来，让我们来表示一下
通过P项我叫进位传递,
被Gi称为携带世代因此方程(i)和(ii)可以改写为
具体地说,
对于i = 0，我们有，
对于i = 1，我们有，
对于i = 2，我们有，
推广一下，对于i = n，我们有，
在上述所有表达式中需要注意的重要因素是，任何特定阶段的进位项只取决于进位输入(c0)项，除了携带生成和携带传播项。是的，只在c上0(用户提供的输入位)，而不是由其前面的阶段生成的进位项。这与他们所处的阶段无关。
这与纹波携带加法器/减法者的情况不同，因为它们具有其目前阶段的携带期限决定其直接前期阶段的携带术语。这种质量进位超前加法器使其克服普通加/减电路的纹波携带传播延迟。
同样的原因使前加器的操作比其他种类的快得多。然而，它所付出的代价是其硬件的复杂性。
