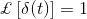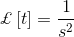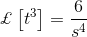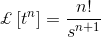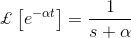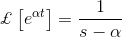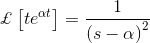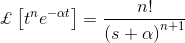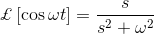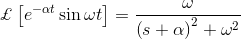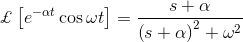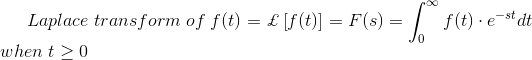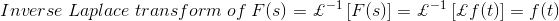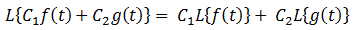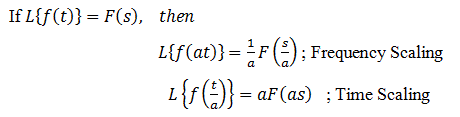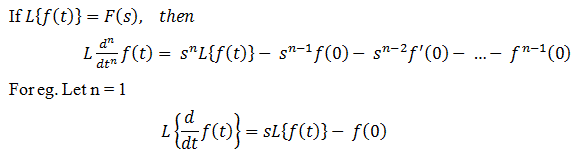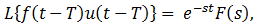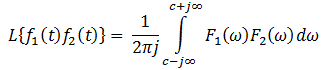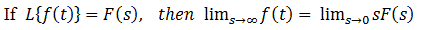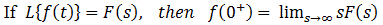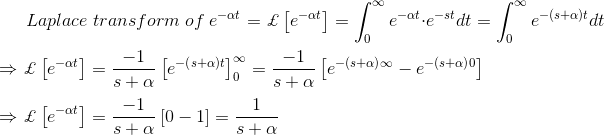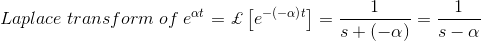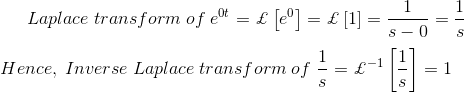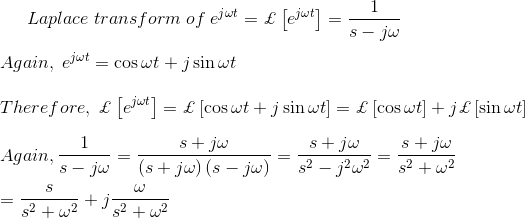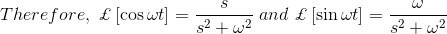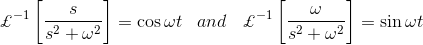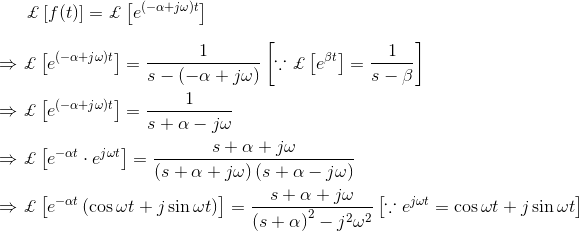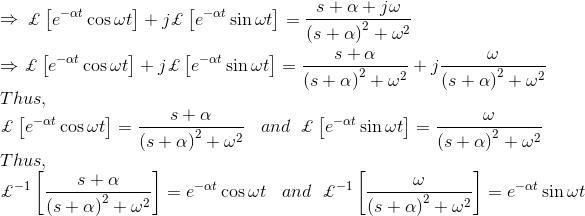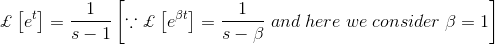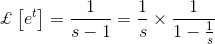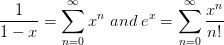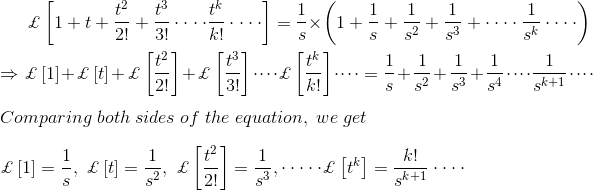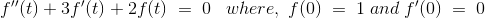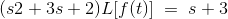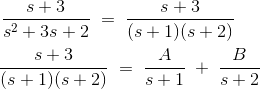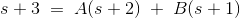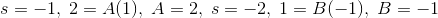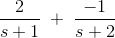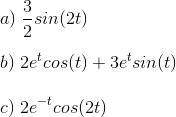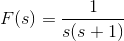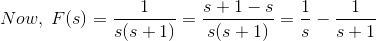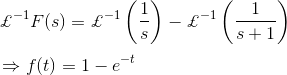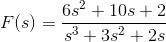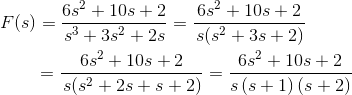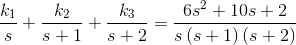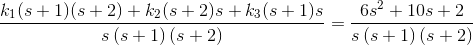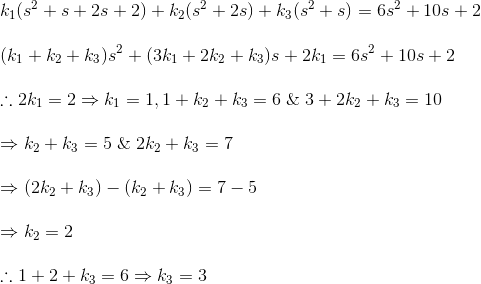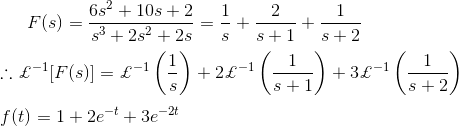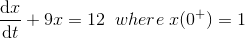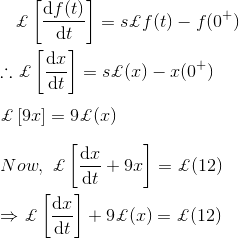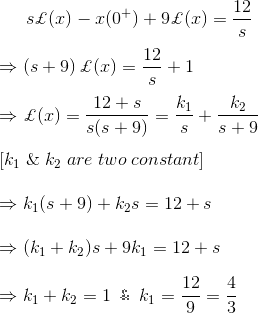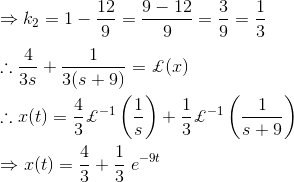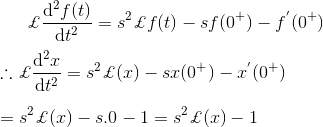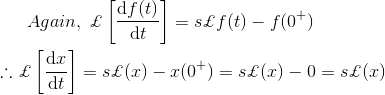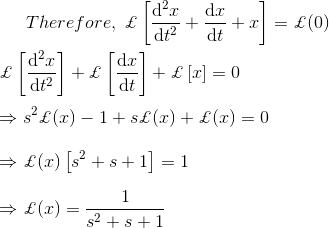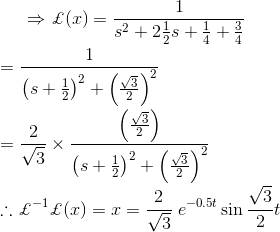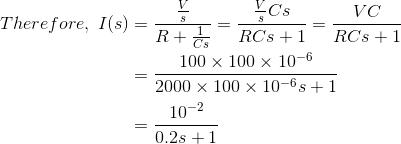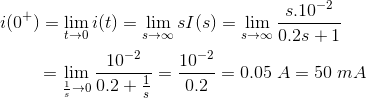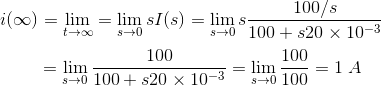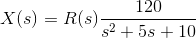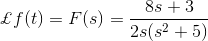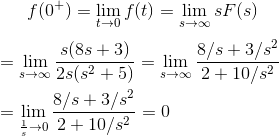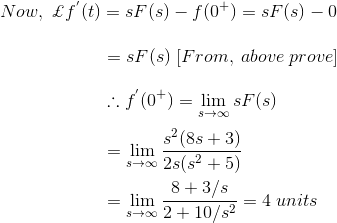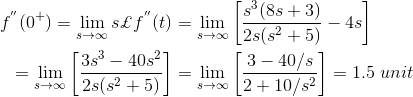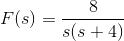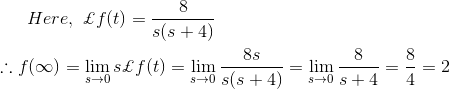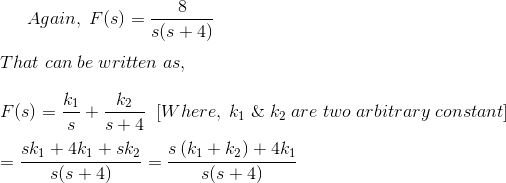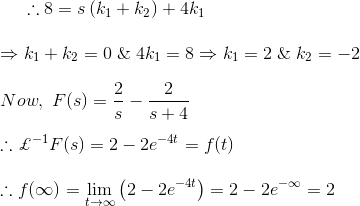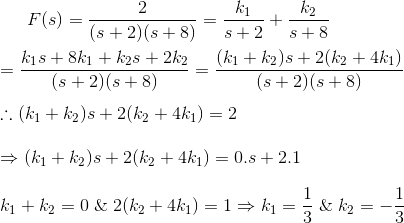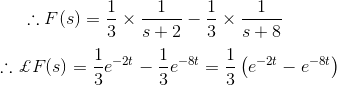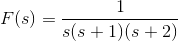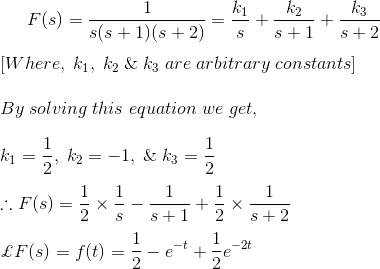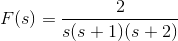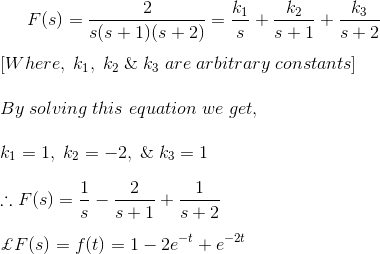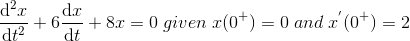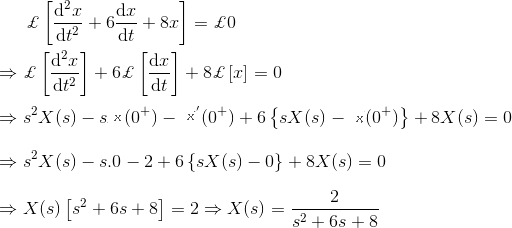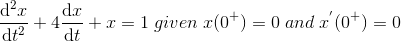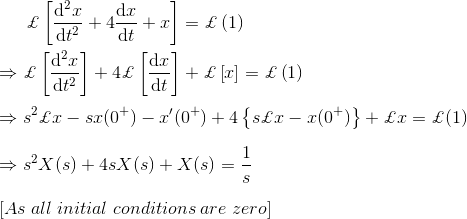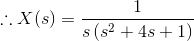拉普拉斯变换是解微分方程的技巧。首先将时域形式的微分方程转化为频域形式的代数方程。在频域上求解代数方程,最后将结果转化为时域形式,从而得到微分方程的最终解。换句话说,可以说,拉普拉斯变换只不过是求解微分方程的一种捷径方法。
在这篇文章中,我们将讨论拉普拉斯变换以及它们是如何被用来解微分方程的。它们还提供了一种为输入-输出系统形成传递函数的方法,但这里不讨论。它们使用模块图等为控制工程提供了基本的构建模块。
很多种类的变换已经存在但是拉普拉斯变换和傅里叶变换是最着名的。拉普拉斯变换通常用于简化微分方程,进入简单且可溶性的代数问题。即使代数变得有点复杂,它仍然比求解微分方程更容易。
拉普拉斯变换表
工程师总能找到一张包含拉普拉斯变换信息的表格。的一个例子拉普拉斯变换表已制作如下。我们将从下表了解各种常用函数的拉普拉斯变换。
拉普拉斯变换定义
在学习拉普拉斯变换时,不仅仅是要了解表格,而且是公式。
为了理解拉普拉斯变换公式,首先设f(t)是t的函数,当t≥0时
f(t)的拉普拉斯变换f(s)可以定义为
只要积分存在。其中拉普拉斯算子s = σ + jω;是实数还是复数j =√(-1)
拉普拉斯变换方法的缺点
拉普拉斯变换只能用于解复杂的微分方程和所有伟大的方法一样,它确实有一个缺点,看起来可能不是很大。也就是说,你只能用这种方法来解常数已知的微分方程。如果你有一个没有已知常数的方程,那么这个方法是没有用的,你必须找到另一种方法。
拉普拉斯变换的历史
数学中的变换处理的是一个函数到另一个函数的变换,而这个函数可能不在同一个域中。变换方法在那些不能直接求解的问题上得到了应用。这种变换是以法国数学家和著名天文学家皮埃尔·西蒙·拉普拉斯的名字命名的。
他在对概率论进行加法运算时也使用了类似的变换。它在第二次世界大战后开始流行。英国电气工程师奥利弗·希弗赛德(Oliver Heaviside)让这一转变变得流行起来。其他著名的科学家如尼尔斯·阿贝尔、马蒂亚斯·勒奇和托马斯·布罗米奇在19世纪也使用过这个词。
拉普拉斯变换的完整历史可以追溯到更早的1744年。这时另一位伟大的数学家莱昂哈德·欧拉正在研究其他类型的积分。然而欧拉并没有深入研究,而是离开了它。欧拉的崇拜者约瑟夫·拉格朗日;对欧拉的工作做了一些修改并做了进一步的工作。拉格朗日的工作在38年后得到了拉普拉斯的注意,1782年,他继续从欧拉离开的地方开始。但不是3年后;1785年,拉普拉斯灵机一动永远改变了我们解微分方程的方式。他继续研究它并不断地发掘拉普拉斯变换的真正威力直到1809年,他开始用无穷作为积分条件。
拉普拉斯变换法
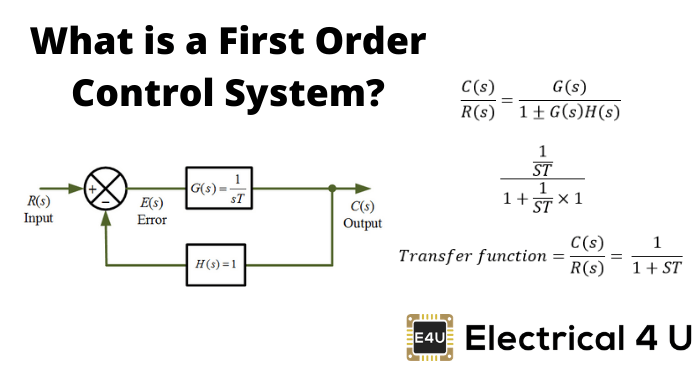
拉普拉斯变换是控制系统工程的重要组成部分。为了学习或分析控制系统,我们必须执行不同功能的拉普拉斯变换(时间功能)。逆拉普拉斯也是从拉普拉斯形式找出功能f(t)的必要工具。逆拉普拉斯和拉普拉斯变换都具有一定的性能在分析动态控制系统方面。拉普拉斯变换有几个用于线性系统的属性。不同的属性是:
线性,微分,积分,乘法,频移,时间缩放,时移,卷积,共轭,周期函数。有两个与控制系统相关的非常重要的定理。这些都是:
对-脉冲函数、单位脉冲函数、阶跃函数、单位阶跃函数、移位单位阶跃函数、斜坡函数、指数衰减函数、正弦函数、余弦函数、双曲正弦函数、双曲余弦函数、自然对数函数、贝塞尔函数等进行了拉普拉斯变换。但应用拉普拉斯变换的最大优点是通过将高阶微分方程转化为代数方程,可以很容易地求解高阶微分方程。
要对时间函数做拉普拉斯变换需要遵循一些步骤。为了将给定的时间函数f(t)变换为相应的拉普拉斯变换,我们必须遵循以下步骤:
- 首先把f(t)乘以e-S,S是复数(S =σ+JΩ)。
- 将本产品W.R.T的时间集成为零和无穷大的限制。该集成导致Laplace变换F(t),其由f(s)表示。
时间函数f(t)是通过拉普拉斯逆变换得到的,记为£-1
拉普拉斯变换属性
拉普拉斯变换的主要性质可以概括为:
线性:让C1C2是常数。f(t),g(t)是时间,t,然后
第一次转移定理:
更改规模财产:
分化:
集成:
时间变化:
如果L (f(t)} = f(s)那么f(t)在延时后的拉普拉斯变换,t等于f(t)和e的拉普拉斯变换的乘积-这是
其中,U(T-T)表示单位步进功能。
产品:
如果L{f(t)}= f(s)那么两个函数的乘积f1(t)和f2(t)是
最终值定理:
本定理适用于反馈控制系统的分析和设计,因为拉普拉斯变换在初始条件下提供解决方案
初始值定理:
我们来研究一个简单函数f(t) = e的拉普拉斯变换方法αt.为了更好地理解这个问题。
比较上述解决方案,我们可以写,
同样,让α = 0,我们得到,
同样地,让α = jω,我们得到,
因此,
我们再来看另一个拉普拉斯变换示例函数的方法
再一次,e的拉普拉斯变换T.是,
这个拉普拉斯形式可以写成
现在从Power系列的定义我们得到,
拉普拉斯变换的例子
使用求解等式拉普拉斯变换那
利用上表,可以将方程转化为拉普拉斯形式:
利用问题中给出的数据,可以简化拉普拉斯形式。
除以(s2+ 3s + 2)给出
这可以使用部分分馏来解决,这比以前的形式更容易地解决它。首先,分母需要要分解。
交叉乘法给出:
接下来需要找到系数a和b
代入方程:
然后利用上面提供的表格,可以将该方程转换回正规形式。
试试自己的例子
计算和写出以下内部的逆拉普拉斯变换,建议在线查找一个带拉普拉斯级的表:
解决方案:
让我们再深入研究一些拉普拉斯变换的例子:
1)式中,F(s)是时域函数F(t)的拉普拉斯形式。求f(t)的到期点。
解决方案
现在,F(s)的逆拉普拉斯变换是
的拉普拉斯逆变换函数
解决方案
现在,
因此,
3)解微分方程
解决方案
正如我们所知,拉普拉斯变换
4)解决微分方程,
解决方案
正如我们所知,
5)对于下面的电路,利用拉普拉斯变换技术计算电容器的初始充电电流。
解决方案
上面的图可以在拉普拉斯形式中重新绘制,
现在,初始充电电流,
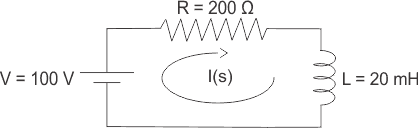
6)解决电路通过使用拉普拉斯变换进行最终稳态电流
解决方案
通过使用可以分析上述电路基尔霍夫电压定律然后我们得到
稳态电流的最终值为
一个系统由关系表示
其中,R(s)是单位步进功能的拉普拉斯形式。在t→∞处找到x(t)的值。
R(s)是单位阶跃函数的拉普拉斯形式,可以写成
解决方案
8)求f(t) f'(t)和f“对于时域函数f(t)函数的拉普拉斯变换形式是
通过应用初始值定理,我们得到,
应用初值定理,我们得到,
f(t)的拉普拉斯变换由,
使用最终值定理找到等式的最终值以及找到最终值的传统方法。
解决方案
因此,证明了函数的最终值的两个方法都变得相同。
求函数的拉普拉斯逆变换,
解决方案
f(s)可以重写为
11)找到反向拉普拉斯变换的
解决方案
f(s)可以重写为
求。的拉普拉斯逆变换
解决方案
f(s)可以重写为
13)用拉普拉斯变换表示微分方程
解决方案
14)用拉普拉斯变换表示微分方程
解决方案
在现实生活中使用的拉普拉斯变换在哪里?
这拉普拉斯变换是由Lerch消去定律推导出来的。在拉普拉斯变换方法中,将时域的函数变换为频域的拉普拉斯函数。这个拉普拉斯函数是一个代数方程的形式,很容易求解。通过拉普拉斯逆变换,可以将解再次变换回时域。
如上所述,该变换最常用于控制系统。变换用于研究和分析通风,加热和空气条件等系统等。这些系统用于每一个现代化的一天建筑和建筑。
拉普拉斯变换对过程控制也很重要。它有助于可变分析,当改变时产生所需的结果。可以在用热量进行实验中找到该示例。
除了这两个例子外,拉普拉斯变换在很多工程应用中都有应用,是一种非常有用的方法。它在电子工程和机械工程中都很有用。
动态控制系统的控制动作是电气,机械,热,液压等的电动,机械,热,液压等可以由微分方程表示。根据物理规律管理,系统微分方程是一个系统。为了便于描述控制系统的微分方程的解决方案,将等式转换成代数形式。这项转变是在帮助的帮助下完成的拉普拉斯变换技术,即时域微分方程被转换为频域代数方程。
一个有趣的类比可以帮助我们理解拉普拉斯。假设你读不懂一首英文诗。然而,你有一个西班牙朋友,他很擅长理解这些诗。所以你把这首诗翻译成西班牙语发给他,他反过来用西班牙语解释这首诗然后再发给你。你理解了西班牙语的解释,然后能够将诗歌的意思转换回英语,从而理解英语诗歌。