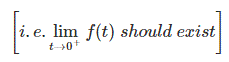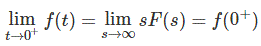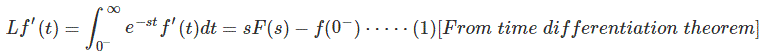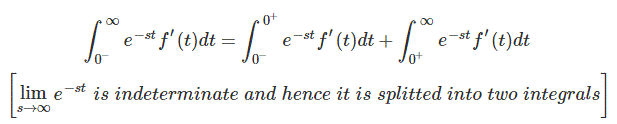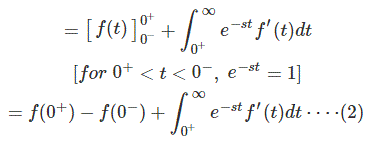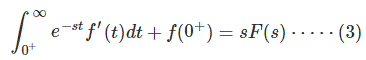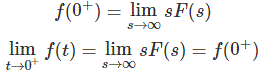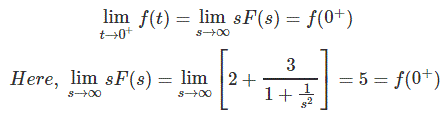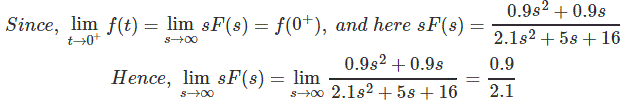拉普拉斯变换的初始值定理

初值定理是基本性质之一拉普拉斯变换。它是由突出的法国数学物理学家皮埃尔西蒙马奎斯德拉普拉斯给出。他通过应用牛顿的引力理论，他在行星运动领域作出了重要贡献。他对概率和统计论理论的工作被认为是开创性的，这影响了全面新一代的数学家。Laplace是72人中有一个名字刻在埃菲尔铁塔上的名字之一。
初始值定理和最终值定理在一起称为限制定理。初始值定理通常称为IVT。它将使我们能够在时间t =（0⁺）对于给定的转换功能（LAPLACE）而不使我们更加努力地找到f（t），在这种情况下是一个繁琐的过程。

初始值定理存在的条件

1. 1. 功能f（t）及其导数f（t）应该是拉普拉斯可变形的。
   2. 如果时间t接近（0⁺）然后应该存在函数f（t）。

1. T> 0的功能f（t）= 0，并且在原点不包含脉冲或更高阶的奇点。

拉普拉斯初始价值定理声明

如果f（t）和f（s）是拉普拉斯变换对。IE

的初值定理

拉普拉斯初始值定理证明

函数f（t）的拉普拉斯变换是

然后拉普拉斯转换为其导数f'（t）是

首先考虑整体部分

替代（2）在（1）中我们得到

消去f (0^-）双方我们得到了

我们可以直接地写下上面的等式，但我的内容就会从（0^-然而，对于∞），我们考虑其与具有正值的结果的限制的负值。

笔记：
我们还知道拉普拉斯变换仅适用于因果职能。
考虑到（S）倾向于（3）的双方都无限

因此，证明了初始值定理。

初始值定理的应用

正如我所说，初始值定理的目的是确定函数f（t）的初始值，所以提供了其拉普拉斯变换
例1：
找到函数f（t）= 2 u（t）+ 3成本U（t）的初始值
索尔:

通过初始值定理

初始值由5表示。
例2：
查找变换功能的初始值

索尔:

通过初始值定理

[由于S→∞S变得越来越微不足道的值，因此通过简单地采用领先的共同效率的比率来获得结果

例3：
找到初始值
解决方案:
在这种情况下，初始值定理不适用。我们可以通过两种方式证明这一点。
让我们看看它是怎么回事
方法1：

笔记：
如果F（s）是适当的级分，则该定理是适用的，则分子多项式比分母多项式较低。
如果应用IVT，我们将获得∞作为初始值。

[在实用电路中是不可能的]
aliter：


应用逆拉普拉斯变换

显而易见的是，由于存在脉冲函数，因此不适用初始值定理，这随着时间的推移是恒定的。

通过本讨论，可以轻松地操纵电路的初始条件，随着拉普拉斯变换功能。