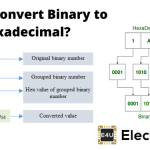
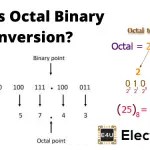
十六进制系统是具有基座16的数字系统。现代计算机系统大大使用该数字系统。我们已经了解了十进制数字系统,二进制数字系统和八进制数系统.与那些称为十六进制数字系统的另一个数字系统。顾名思义,此数字系统中有16个符号从0开始。
在解释数字系统之前,我们应该知道这个数字系统为什么会存在。使用十进制是人类的自然趋势,因为0的使用非常简单,操作也很友好,所以人们对它很熟悉。而计算机系统早先使用的是二进制系统,因为只有两种状态:开和关。
但是随着人们对计算机的依赖越来越大,需要开发不同的数学程序和软件,就需要开发一种基数大于十进制的数字系统,选择16是因为比特,字节是它的倍数。现在HTML和CSS中使用了这个数字系统,使用了十六进制表示法。这个数字系统最早是在1956年左右的Bendix G-15计算机上使用的。
现在来代表十六进制数字系统,在该号码系统中,有16个基本数字可以表示所有数字,这些是0,2,3,4,5,6,7,8,9,a,b,c,d,e,f前10位类似于十进制数系,但是最后6位数分别表示10,11,12,13,14和15。十六进制号码中的任何数字都可以很容易地转换为其他数字系统的数量,在下一篇文章中给出了过程。
在十进制系统中,我们使用符号1和0并排,即10表示••••••••••
就是9 + 1。之后是11,然后是12,以此类推。这意味着,在9或9之后,我们把左边的第一个非零数字(即1)带回来,在它的右边重复从0到9的所有符号,以表示从10到19(10 - 19)的下十个更高的数字。在19之后,我们把2放在左边,然后再重复0到9来代表接下来的10个更高的数字,从20到29(20 - 29)。
十进制数系统是非常基本的数字系统,因为十个符号或数字以不同的组合使用来表示所有数字,该系统被称为基数十(10)。现在考虑一个数字系统,您被告知使用十六个符号而不是10个符号。那么你的新号码系统的基本建设将是什么?首先,我们必须找出16个符号来表示该新数字系统的基本数字。
我们可以为此创建新系列的符号,但如果我们这样做,那将是非常困难的。如果我们使用常用的符号为此目的,可以解决这种困难。因此,我们可以简单地使用0到9个十进制系统来表示该新数字系统的前十位数0到9。
但是其他6位高的数字在十进制中没有符号,所以我们必须从一些常用的系统中寻找它们。我们可以很容易地从字母系统中得到它们,这意味着我们可以使用A, B, C, D, E和F作为在这个新的数字系统中从10到15的下6个更高的数字。总共使用16个基本数字的系统称为十六进制数字系统。
| 一个♥. | • | • | • | • | • | • | • | • | • | • | |||||
| B⇒ | • | • | • | • | • | • | • | • | • | • | • | ||||
| C⇒ | • | • | • | • | • | • | • | • | • | • | • | • | |||
| d⇒ | • | • | • | • | • | • | • | • | • | • | • | • | • | ||
| e⇒. | • | • | • | • | • | • | • | • | • | • | • | • | • | • | |
| F⇒ | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • |
在十六进制中,我们用16个符号来代表所有的数字。这些符号是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E和F。F之后,我们用10表示下一个更高的数字16。然后下一个增量是11,用来表示下一个自然数17,以此类推。
因此在F之后的十六进制系统中,第一位数变为1,第二位数将由0到F一个接一个地重复,以表示自然数16到31。
这意味着,10‰16,1117,12⇒18,13⇒19,14°20,15°21,112,17℃,18°24,19℃,1a⇒26,1b⇒27,1c⇒28,10⇒29,1e⇒30,1f⇒11。在此之后,第一位数将增加到2,再次将第二位数逐一重复0到f,以表示自然数32至47等。
十进制到十六进制的转换
由于我们已经在以前的文章中陈述了数字系统的所有数字系统,所以所有数字系统都是相关的,所以作为十进制和十六进制数。就像你一样将十进制数转换为二进制数,或将十进制数转换为八进制数,十进制数系统中的任何数都可以转换为十六进制数系统。
通过逐步示例,很容易理解此过程。
让我们先取一个小数——假设我们取了7510现在我们要把它变成十六进制数,首先要除以16。
75/16 =商4,余数11
因为商小于16,我们就讲到这里,等价的十六进制数是
4B.8= 75.10
现在我们将讨论稍大的数字的方法,
假设这个数字是169310
然后除以16
1693/16 = Quotience = 105,余数= 13(D)
现在我们再把商除以16,看结果
105/16 =商= 6余数= 9
由于商小于16,计算部分就完成了,我们现在可以直接写出结果了
169310d = 6916
因此十进制数已被转换为十六进制数。
从上面的解释可以理解,十六进制数是不同数字与各自乘数乘积的和。乘数是160,161,162,......从右手侧或列出有效位(LSB)。让我们有一个例子4d2,这将被表示为
如果我们划分十进制1234到16时,我们将获得77次,因为余数。然后,如果我们将十进制77分为16,我们将获得4个额外数量和13或D.现在,如果我们从最后一批向第一节写入第一次提醒我们将获得4d2,这是十六进制或十六进制相当于数字1234。
| 用1234除以16得到商77余数2。 | 16 | 1234 | →2 |
| 77再除以16,得到商是4余数是13 D。 | 16 | 77. | →D |
| 4 |
向十进制转换的视频演示
十进制转换十六进制
以类似的方式可以将任何十六进制数转换为十进制数。我们将使用一个例子调查该过程。
但之前应该明确表示,十六进制数转换之前的所有字母数字应被视为在十进制数数值系统,即如果一位十六进制数是一个我们需要10,现在一个例子会使整个过程清晰。
让我们采取任何十六进制数字45b116,我们必须将其转换为十进制数,因此从最正确的最初数字开始,我们必须开始将数字乘以16从0开始的升序。
所以被拿走的号码将被操作为
在此过程中,任何十六进制数可以转换为十进制数。
通过将十六进制数的每个数字乘以其各自的乘法器来确定值十六进制数。我们从LSB开始或最正确的数字并将其乘以160然后将在LSB左侧的下一个数字上来并将其乘以161之后,我们来到了另外的左数字并乘以162用它。我们将其持续到MSB或最遗留的位置。添加所有此产品,最后我们获得十进制相当于十六进制数。这一个最简单的过程十六进制到十进制的转换.
想想十六进制数4D2。这里数字的最低有效位是2所以我们将它与16相乘0或1。然后左边的下一位是D或13我们将它乘以161或16。最后我们将最左边的数字乘以MSB,即4乘以162.现在如果我们把这三项加起来,最后我们会得到相当于这个十六进制数的十进制数。这就是十六进制到十进制的转换
因此,