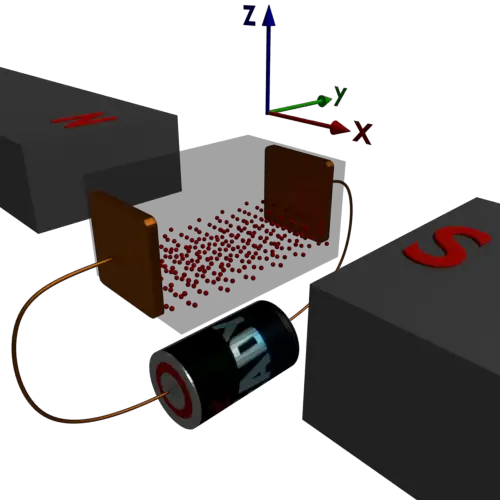
主要是洛伦兹力量负责霍尔效应．我们都知道当我们放a的时候磁场内的载流导体，导体对取决于方向的方向体验机械力磁场以及电流在导体中的方向。这电流表示电荷的流动。在金属中，这完全是由于电子的流动半导体，它是由于自由电子流以及孔。在半导体中，孔在常规电流的方向上移动，并且自由电子在与常规电流的方向相反。当电子有充电时，它们在流过时遇到力量导体放在磁场内。由于这种力，电子在流动期间朝向导电的一侧转移。由于以下电荷移至导体的一侧，因此导体的横截面上可能存在微小的电位差异。我们称之为霍尔效应的整个现象。
让我们占据一块金属，如下所示。我们在这里显示它作为更好的理解透明。
后应用电压通过电流，“I”开始沿x方向从左向右流动。我们将金属块置于密度为B的磁场中。磁场的方向沿着y轴。现在根据弗莱明左手规则，载流子将经历一个力取决于两个方向的电流和方向磁场．根据熔普明的规则，导通电子将朝向块的底部偏转。结果，块的上部和下部的电子浓度将存在变化。因此，沿z轴横跨块出现微小的电位差。这电场由于这种电极的这种换档而产生的也与电子朝向金属块的表面相反。因此，可能有两种力作用于电荷载体。
- 由于霍尔效应导致的力量
- 由于产生的电场而导致的力量
这些力彼此相反。建立某些电场后霍尔效应该系统变得均衡。在该条件下，由于所建立的电场和由于霍尔效应，作用在电荷载体（传导电子）上的力变得相同。因此，朝向块的表面上没有进一步改变电子，并且系统变得平衡状态。
让我们专注于一支电荷载体移动导体放在磁场内。
电荷载体的电荷是E（例如）
磁场的磁通量密度为B(说)。
现在我们可以在有效长度L和电流I的电流承载导体上写入作用的磁力。
当B和I的方向相互垂直。
我们可以将上述等式重写为
其中V是通过导体的电荷的速度。
从上面的等式中，我们可以在单一充电载体上写出作用的力量，
其中V是电荷载体的漂移速度。
现在我们可以写由于霍尔效应as，E.H．
因此，我们可以根据现场写在充电载体上的力
现在均衡
现在我们考虑N是载流子浓度。
从方程1和2，我们可以写出
我们称之为这个词
作为霍尔效应的系数或霍尔系数。我们将霍尔系数定义为每单位电流密度的单位磁场密度的霍尔场。
霍尔效应的应用
霍尔效应是一个非常有用的现象并有助于
确定半导体的类型
通过知道霍尔电压的方向，就可以确定给定的样品是否n型半导体或P型半导体．这是因为霍尔系数对于n型半导体是负的，而在p型半导体的情况下相同是正的。
计算载流子浓度
在霍尔系数方面给出了电子（n）和孔（p）的载流子浓度的表达式
确定机动性(霍尔机动性)
电子(μ)的迁移率表达式N)和孔(μP.）以霍尔系数表示，由此表示，
在哪里，σ.N和σ.P.代表这一点电导率由于电子和孔。
测量磁通量密度
可以从霍尔电压的等式中容易地推导出该等式，并由
此外，市面上有许多基于霍尔效应原理的设备，包括霍尔效应传感器和霍尔效应探针。
