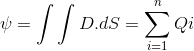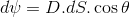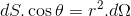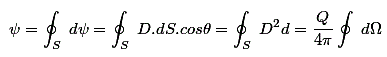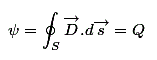高斯定理

我们知道，围绕正电荷或负电荷围绕静电场，并且在该静电场中存在能量管的流量或助势。实际上这一点助势从电荷辐射/散发。现在这种通量流量的量取决于它从其发出的电荷量。找出这一关系，高斯的定理介绍了。本定理可以被认为是电气科学领域中最强大和最有用的定理之一。我们可以从本定理中发现通过围绕电荷的表面区域辐射的磁通量。

这个定理说明了总数电量通过围绕电荷的任何闭合表面，等于该表面包围的净正电荷。
假设收费Q₁，问：₂_ _ _ _Q_一世，_ _ _ q_N由表面括起来，然后定理可以通过表面积分在数学上以数学方式表达

在哪里，d是助势coulombs / m中的密度²而DS是向外指向的矢量。

高斯定理的解释

用于解释这一点高斯的定理，最好经历一个正确的理解。
让q成为球体中心的电荷和助势从充电散发到表面上。现在，这个定理说明了总数助势从充电中散发出等于Q库仑，这也可以在数学上证明。但是当充电没有放置在中心时，但在中心以外的任何点（如图所示）。

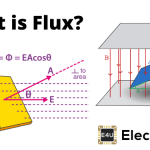
此时，磁通线对电荷围绕的表面不正常，然后将该焊剂分解为彼此垂直的两个部件，水平的是SINθ分量，并且垂直是COSθ分量。现在，当这些组件的总和进行所有费用时，网络结果等于系统的总收费高斯的定理。

高斯定理证明

让我们考虑位于允许介质的同质各向同性介质中的点电荷Q。

这电场强度从充电的距离r的任何点都是

这通量密度被给出，

现在来自图助势通过区域DS.

其中，θ是d和正常到ds之间的角度。
现在，DSCOSθ是DS的投影到达半径向量。通过定义实心角度

其中，DΩ是由基本表面下Q下调的实心角是DS。所以总流离失所助势通过整个表面积是

现在，我们知道，通过任何封闭表面赋予的固体角是4π的斯特拉迪人，因此整个表面的总电量是

这是一体的形式高斯的定理。因此，证明了本定理。