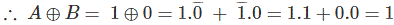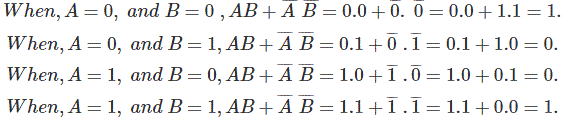内容
什么是异或门?
XOR门(也称为EOR或EXOR GATE) - 发音为独占或门 - 是一种数字逻辑门,当真正输入的数量是奇数时,一个数字逻辑门给出真实(即高或1)输出。XOR门实现一个独占的,即,如果一个 - 且只有一栅极的输入为真,则会发生真正的输出结果。如果两个输入都是假(即,低或0)或两个输入为真,则输出为false。
XOR表示不等式函数,即,如果输入不一样,则输出为真;否则,输出是假的。记住XOR的常见方式是“必须有一个或另一个,而不是两个”。
另一种看待异或门的方法是:二元系统中两个变量的模和是这样的:
逻辑门执行该模型和操作而不包括携带被称为XOR门.XOR门通常是两个输入逻辑门,其中输出仅是逻辑1当只有一个输入是逻辑1时。当两个输入相等时,均为1或两个都是0,输出将是逻辑0。
这就是为什么XOR门也称为反符合门或不等式检测器。这个门被称为异或或排他或门因为当它的输入只有1时,它的输出只有1。
在数字电子技术,其他逻辑门包括不是盖茨那或门那NAND盖茨,盖茨也不.
XOR门真相表
真值表列出特定数字逻辑电路的输出,以了解其输入的所有可能组合。这真值表XOR门如下:
上述真值表的二进位运算称为排他或运算。用A⊕b表示。异或运算的符号用一个圆圈⊕所环绕的正环表示。
XOR门电路图
上式A⊕B可简化为:
让我们证明上面的表达式。
在第一种情况下,考虑A = 0和B = 0。
在第二种情况下,考虑A = 0和B = 1。
在第三种情况下考虑,a = 1和b = 0。
在第四种情况下,考虑A = 1和B = 1。
因此证明了A⊕B的布尔表达式为AB̅+ ĀB,因为这个布尔表达式满足关于an的所有输出状态XOR门的输入条件.
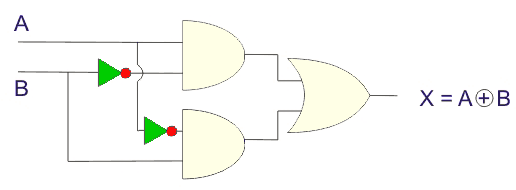
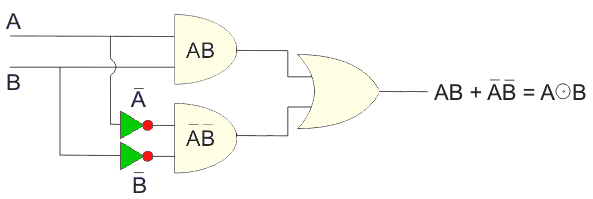
从这种布尔表达式中,可以轻松实现XOR门的逻辑电路,这将如图所示,
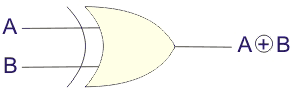
异或门的逻辑符号
XOR门逻辑地表示为,
多输入XOR门
虽然XOR门只能有两个输入,但您可以使用任意数量的输入执行XOR操作(例如,输入XOR操作或4输入XOR操作)。
两个以上的输入XOR操作是,当栅极区域1中的奇数数量时,输出为1,当没有或甚至输入的数量为1时,输出是逻辑0。
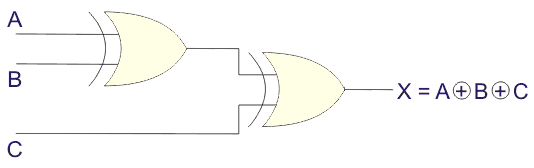
3输入XOR门
让我们实现一个具有三个输入A、B和C的异或门。
现在,根据有三个以上输入的异或操作的定义,真值表会,
这个真理表可以阐述,
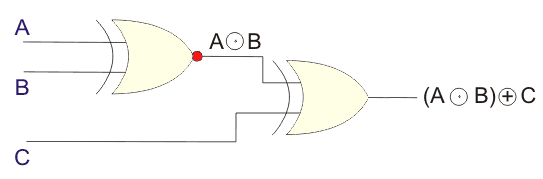
从上述真相表中,发现三个二进制变量的XOR操作等同于一个变量的XOR操作,以及其他两个变量的XOR操作的结果。
从上面的真相表,
什么是Xnor门?
XNOR门(也称为Xorn't,Enor,Exnor或Nxor) - 并发音为独占式,也不是 - 是一种数字逻辑门,其功能是异或门(XOR门)的逻辑补充。逻辑上,一个xnor门是A.不是门后面是异或门。
输入A和B的XOR操作是A≠B;因此,XNOR操作这些输入将是(A + B)̅。这意味着XOR门的输出在Xnor门中反转。
在异或门操作中,当只有一个输入为1时,输出只有1。当两个输入相同时,输出是逻辑0,这意味着它们要么是1,要么是0。但在XNOR门中,逆是正确的。因此,当只有一个输入为0时输出为0,当两个输入都相同时输出为1(即两个0或两个1)。
请参阅下面的Xnor Gate Truth表中的视觉表示。
Xnor门真相表
这真值表的Xnor门如下所示:
逻辑XNOR操作由⊙表示。这是一个被圆圈包围的点。变量A和B之间的XNOR操作的表达式表示为⊙B。
现在,真相表对等式ab +Âb̅表示满意。
由此证明了A⊙B = AB + ĀB̅。同样的可以用使用来证明k-map.还。
XNOR门电路图
通过使用两个可以实现XNOR操作的表达不是盖茨, 二和盖茨和一个人或门作为追随者,
Xnor门的符号:
3输入xnor门
就像XOR门,Xnor门仅存有两个输入,但对于具有多个以上的输入的XNOR操作,我们必须使用多个Xnor门。
具有两个以上输入的XNOR操作就是这样。当高或逻辑1条件下有奇数输入时,输出将为0;否则,输出将为1。
现在,
从这个精心的真理表中,三个输入xnor门的逻辑符号可以表示为,
XOR门的应用
排他或门的主要应用是在运行中半和全加法器.如果我们看真值表仔细,我们会发现前三个结果完全满足过程二进制添加.然而,在最后一个输入序列中,即当两个输入都为1时,根据加法规则,结果应该是0,进位1。在真值表中,我们得到了期望的0,但缺少了1。
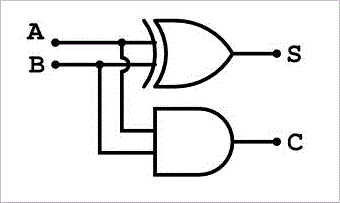
要在设计加法器的电路时解决此问题,请将AND AND添加到前或门在平行下。我们将详细展示加法器的电路。
从上图中,我们可以看到,在半加法器电路中,两个输入并行地通过异或门和与门。通过这个电路的运算,我们得到了二进制添加顺利。
伪随机数生成-建立线性反馈模型移位寄存器,前或门,并产生一个随机序列的比特。