等效电阻:什么是等效电阻?如何找到等效电阻betway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

什么是等效电阻?

的等效电阻被定义为一个点，其中总电阻是用平行或系列电路(在整个电路或电路的一部分)。等效电阻定义在两个或两个终端之间节点的网络。等效电阻可能听起来很复杂，但这只是“总电阻”的一种技术说法。

在网络的等效电阻中，单个电阻电阻器可以用完整的网络来代替一个特定的应用吗电压和/或等价的当前的作为网络使用时，可以得到类似的结果。

当一个电路中有多个电路元件时，应该有一种方法来计算整个电路或电路的一部分的总有效电阻。

在讨论什么是等效电阻之前，我们先来描述一下电阻。电阻是一种衡量装置或材料抵抗流过它的电流的能力的指标。与电流成反比，电阻越大，电流越小;电阻减小意味着电流增大。

如何找到等效电阻

等效电阻表示电路中所有电阻器的总效应。等效电阻可以在串联或并联电路中测量。

电阻器由两个结组成，电流通过两个结和两个结。它们是利用电力的无源装置。为了提高净电阻，电阻器必须串联，电阻器必须并联，以减小电阻。

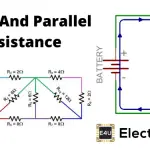
等效电阻并联电路

并联电路是指元件连接到不同的支路上的电路。在并联电路中，每个并联支路的电压降是相同的。每个支路内的总电流等于支路外的总电流。

电路的等效电阻是单个电阻器为了使电路中存在的一组电阻器的总效应相等所需要的电阻量。对于并联电路，并联电路的等效电阻为

${对齐*}\ \开始压裂{1}{R_p} = \压裂{1}{R_1} + \压裂{1}{R_2} + \压裂{1}{R_3} +……+ \压裂{1}{R_n} \{对齐*}结束$

在哪里 $R_1$ ， $R_2$ , $R_3$ 为并联的单个电阻器的电阻值。

总电流往往与累积电阻的大小成反比。单个电阻的电阻和电阻集合的总电阻之间有直接的关系。

如果电阻器的所有端点都连接到电力供应，因此电阻并联，它们的等效电阻在它们的端点之间下降。并联电路电流有多个方向流动。

为了研究这一关系，让我们从两个并联支路的最简单的情况开始，每个支路的电阻值都与4相同 $\ω$ ．由于该电路提供了两个等效的电荷传输路径，因此只有一半的负责可选择通过分支机构进行旅行。

虽然每个分支给出4 $\ω$ 对于通过它的电荷的电阻，只有一半通过电路的电荷会遇到4 $\ω$ 抵抗那支树枝。因此，存在两个4 $\ω$ 并联的电阻等于1个2 $\ω$ 电路中的电阻。这就是并联电路中等效电阻的概念。

等效电阻串联电路

如果所有元件串联，则电路称为串联电路。在串联电路中，每个单元都以这样一种方式连接，使电荷只能通过一条路径通过外部电路。通过外部电路回路的每一个电荷都将按顺序通过每个电阻。在串联电路中，电流只有一条通路流动。

电荷在外部电路中以相同的速率流动。水流并不是某一处强而另一处弱。相反，电流的确切数量随着总电阻的变化而变化。在电路中，单个电阻的电阻和所有电阻的总电阻之间有直接的关系。

例如，当两个6-Ω电阻串联时，就相当于电路中有一个12-Ω电阻。这就是串联电路中等效电阻的概念。

对于串联电路，串联电路的等效电阻为

$\begin{align*} R_s = R_1 + R_2 + R_3 + ....结束R_n \{对齐*}$

如果一个电阻的端点与相邻电阻的端点线性连接，并且一个电阻的自由端和另一个电阻的自由端连接到电源上。然后把两个电阻串联起来，它们的等电阻在两端之间增大。

等效电阻的例子

对于所示的电阻组合，求A点和B点之间的等效电阻。

示例1

对于下面给定的电路，点A和点B之间的等效电阻是多少?

这两个电阻 $R_1$ 和 $R_2$ 与价值 $4 \ω$ 在系列。因此，它们的等效电阻值为

$\begin{align*} R_s = R_1 + R_2 \end{align*}$

$\begin{align*} R_s = 4\ ω + 4\ ω = 8\ ω \end{align*}$

$R_s$ ， $R_3$ 和 $R_4$ 在并行。电路的等效电阻。

${对齐*}\ \开始压裂{1}{R_p} = \压裂{1}{8ω\}+ \压裂{1}{6ω\}+ \压裂{1}{4ω\}= \压裂{13}{24}\ω\{对齐*}结束$

${对齐*}\ \开始压裂{1}{R_p} = 1.85ω\ \{对齐*}结束$

示例2

对于下面给定的电路，计算A和B端点之间的等效电阻

串联电阻的等效电阻表达式如下:

$\begin{align*} R_s = R_1 + R_2 +R_3\end{align*}$

${begin{align*} R_s = 2\ ω + 3\ ω +4\ ω \end{align*}$

$\begin{align*} R_s = 3\Omega\end{align*}$

哪个电路等效电阻最小

示例1

根据下面给出的电路，找出具有最小等效电阻的电路。

第一个给出的是串联电路。所以等效电阻是

$R_s = 2\Omega + 2\Omega\ = 4\Omega \end{align*}$

第二个给出的是一个并行电路。所以等效电阻是

${对齐*}\ \开始压裂{1}{R_p} = \压裂{1}{2ω\}+ \压裂{1}{2ω\}= 1 \ω\{对齐*}结束$

第二个给出的也是一个并行电路。所以等效电阻是

${对齐*}\ \开始压裂{1}{R_p} = \压裂{1}{1ω\}+ \压裂{1}{1ω\}= 0.5ω\ \{对齐*}结束$

第四个给出的是串联电路。所以等效电阻是

$R_s = 1\Omega + 1\Omega\ = 2\Omega \end{align*}$

因此，由以上计算可知，第三种方案的等效电阻值最小。

困难的等效电阻问题

示例1

求给定电路的等效电阻。

为了得到等效电阻，我们将电阻串联或并联起来。在这里, $6 \ω$ 和 $3 \ω$ 在并行。所以等效电阻是

${对齐*}\ \开始压裂{6 \ times3}{6 + 3} = 2ω\ \{对齐*}结束$

此外, $1 \ω$ 和 $5 \ω$ 电阻是串联的。因此等效电阻为:

${begin{align*} 1\Omega + 5\Omega = 6\Omega\end{align*}$

还原之后，我们注意到， $2 \ω$ 和 $2 \ω$ 是串联的，那么等效电阻呢

$\begin{align*} 2\ ω + 2\ ω = 4\ ω \end{align*}$

这 $4 \ω$ 电阻器现在与 $6 \ω$ 电阻。所以它们的等效电阻是

${对齐*}\ \开始压裂{4 \ * 6}{4 + 6}= 2.4ω\ \{对齐*}结束$

现在用适当的值替换上述电路，这三个电阻将是串联的。因此，最终等效电阻为

$R_{eq} = 4\Omega + 2.4\Omega + 8\Omega = 14.4\Omega \end{align*}$

示例2

点A和点B之间的等效电阻是多少?

为了求通过电池的电流，我们需要求出电路的等效电阻。总电流I被分成 $I_1$ 和 $I_2$ ．当前的 $I_1$ 经过两个 $10 \ω$ 电阻器串联时具有相同的电流。当前的 $I_2$ 通过 $10 \ω$ 和 $20 \ω$ 电阻，因为它们有相同的电流。

我们需要找到电流 $I_2$ 首先计算通过电池的电流I。

我们可以看到, $10 \ω$ 和 $20 \ω$ 电阻是串联的。我们用电阻为的等效电阻器代替它们

$R_{eq} = 10\Omega + 20\Omega = 30\Omega \end{align*}$

两个 $10 \ω$ 电阻是串联的。我们用等效电阻来代替

$R_{eq} = 10\Omega + 10\Omega = 20\Omega \end{align*}$

现在我们有两个电阻 $30 \ω$ 和 $20 \ω$ 并行连接。我们可以用一个等效电阻代替。

${对齐*}\ \开始压裂{1}{R_ {eq}} = \压裂{1}{30}+ \压裂{1}{20}= \压裂{1}{12}\ω\{对齐*}结束$

最后，我们有两个电阻 $10 \ω$ 和 $12 \ω$ 串联连接。这两个电阻器的等效电阻是

$R_{eq} = 10\Omega + 12\Omega = 22\Omega \end{align*}$

现在我们可以找到通过电池的电流。它是什么,

${对齐*}I = \ \开始压裂{V} {R_ {eq}} = \压裂{40}{22}= 1.8安培\{对齐*}结束$

这个电流被分成两股 $I_1$ 和 $I_2$ ．所以总的电流

$\begin{align*}I = I_1 + I_2\end{align*}$

（1） $\begin{equation*}1.8 = I_1 + I_2\end{equation*}$

第二个方程，与电流有关，是电阻两端的电压 $30 \ω$ 等于电阻上的电压 $20 \ω$ ．

（2） $20 \ \开始{方程*}* I_1 = 30 \ * I_2 \{方程*}结束$

由上式(1)和(2)可知电流 $I_2$ 是发现。

$\begin{align*}I_1= 1.8 - I_2\end{align*}$

然后将这个关系式代入式(2)，

$\begin{align*}20(1.8 - I_2) = 30\times I_2 \end{align*}$

$\begin{align*}36 = (20+30)I_2 \end{align*}$

${对齐*}I_2 = \ \开始压裂{36}{50}= 0.72 \结束{对齐*}$

那么现在电流I_1是

$\{对齐*}开始I_1 = 1.8 - 0.72 = 1.08 \结束{对齐*}$