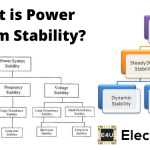
首先我们要知道功率稳定研究。稳定性研究是确定系统在某些扰动下的稳定性的过程,随后是几个开关动作(ON和OFF)。在电力系统这些扰动会对同步电机的性能产生一定的影响。在稳定性研究中对这种影响的评价是暂态稳定研究和稳态稳定性研究。的稳定状态稳定研究了当系统受到小扰动时,系统是否保持了同步。暂态稳定性研究表明,当系统受到较大或较严重的扰动时,系统是否保持同步。
这些扰动可能是短路、应用或突然的大负载损失或发电损失。本研究的目的是研究在消除干扰后,负载角是否恢复到稳定值。本文通过求解非线性方程来确定其稳定性。的同等面积标准与暂态稳定性有关。这实际上是一种非常简单的图形方法。它是为了确定单机或双机系统在无限母线下的暂态稳定性。
稳定等面积准则
通过无损线路,传输的实际功率将是
考虑一个故障发生在同步机器在稳定状态下运行。在这里,能量是由
清除故障时,使用断路器在断层段必须打开。这个过程需要5/6个周期,后续的故障后暂态将需要额外的几个周期。
给输入动力的原动机是由汽轮机驱动的。对于涡轮质量系统,时间常数是在几秒的顺序,而对于电气系统,它是在毫秒。因此,当发生电瞬变时,机械功率保持稳定。暂态研究主要考察了系统的性能电力系统从故障中恢复,并以一个新的可能负载角(δ)提供稳定的功率。
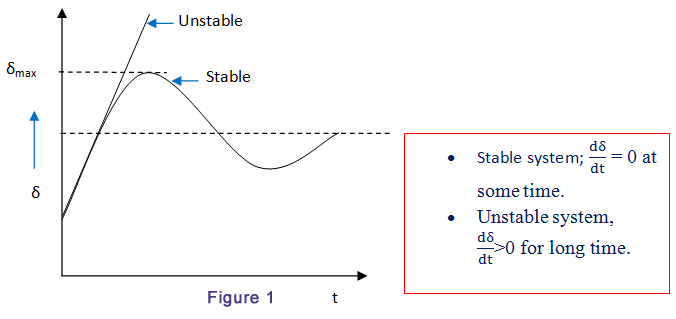
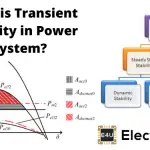
考虑功率角曲线,如图1所示。想象一个提供“P”的系统米打开δ角0(图2)工作在稳态。故障发生时;断路器断开,实际功率降为零。但P米会稳定。因此,加速动力,
功率差异将导致在转子质量中存储的动能的变化率。因此,由于非零加速功率的稳定影响,转子会加速。因此,负载角(δ)将增加。
现在我们可以考虑角δc此时断路器重新合闸。然后功率将回到通常的运行曲线。此时,电功率会高于机械功率。但是,加速度(P一个)将是负的。因此,机器将得到减速。由于转子质量的惯性,负载功率角仍将继续增加。这种增加的负载功率角将停止在适当的时间和转子的机器将开始减速,否则系统的同步将失去。
秋千方程由
P米→机械功率
Pe→电能
δ→负载角
H→惯性常数
ω年代→同步转速
我们知道,
将方程(2)代入方程(1)得到
现在,把dt乘到方程(3)的任意一边,然后在两个任意载荷角δ之间对其积分0和δc.然后我们得到了,
当负载角为δ时,假定发电机处于静止状态0.我们知道
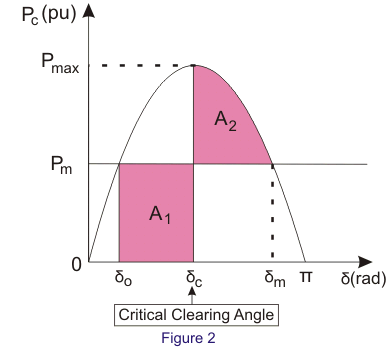
当出现故障时,机器将启动加速。当故障被清除后,它将继续增加速度,直到达到其峰值(δc).在这一点上,
从方程(4)开始加速的面积是
同样,减速面积为
接下来,我们可以假设线路在负载角δ处重新闭合c.在这种情况下,加速度面积大于减速面积。一个1>一个2.发电机的负载角将通过δ点米.超过这一点,机械动力大于电力,它迫使加速动力保持正。在减速之前,发电机因此得到加速。因此,系统将变得不稳定。
当一个2>一个1,系统将在再次加速之前完全减速。在这里,转子的惯性将迫使连续的加速和减速区域比前一个变小。因此,系统将达到稳定状态。
当一个2=一个1,稳定极限的裕度由此条件定义。这里,清除角由δ给出cr,临界净空角。
因为,一个2=一个1.我们得到了
临界清净角与面积相等有关,称为同等面积标准.它可以用来求出系统在不超过稳定极限的情况下所能获得的最大载荷极限。