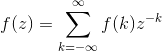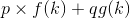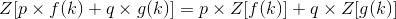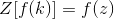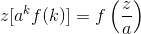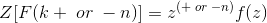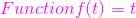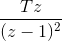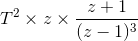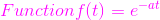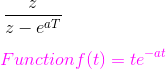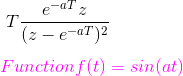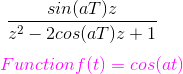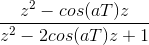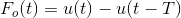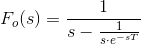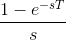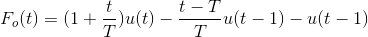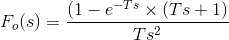在本文中,我们将讨论由离散数据或采样数据组成的离散信号,或者也称为控制系统的数字数据.现在在我们详细讨论这个话题之前,知道是非常重要的,虽然我们有模拟系统,但数字技术的需要是什么?
因此,让我们在模拟系统中讨论数字系统的首先优点。
- 与模拟系统相比,数字系统的功耗较少。
- 数字系统可以轻松处理非线性系统,这是最重要的优势控制系统中的数字数据.
- 由于这一点,数字系统在逻辑运营中展示了逻辑运营,它们显示了在当前世界世界世界中非常有用的决策。betway网页版
- 与模拟系统相比,它们更可靠。
- 数字系统体积小,重量轻,易于使用。
- 它们的工作原理我们可以根据我们的需求进行编程,因此我们可以比模拟系统更通用。
- 在数字技术的帮助下,各种复杂的任务可以很容易地完成,而且精度很高。
假设你有一个连续信号那么你如何把这个连续信号转换成离散信号呢?通过抽样过程,这个问题的答案非常简单。
抽样过程
采样过程是指在开关(也称采样器)的帮助下,将模拟信号转换为数字信号的过程。采样器是一个连续的ON和OFF开关,它直接将模拟信号转换为数字信号。根据所使用的信号的转换,我们可以将采样器串联起来。对于理想的采样器,输出脉冲的宽度非常小(趋近于零)。当讨论离散系统的时候知道z变换是非常重要的。我们将在这里讨论离散系统中的z变换及其应用。z变换在离散系统中的作用与傅里叶变换在连续系统。现在我们来详细讨论z变换。
我们定义z变换为
其中,f(k)是离散数据
Z是复数
f(z)是f(k)的傅立叶变换。
z变换的重要性质如下
线性
让我们考虑两个离散函数f (k)和g (k)的和
使p和q是常数,现在求拉普拉斯变换根据线性性质我们有:
缩放变化:让我们考虑一个函数f(k),以便采取z变换我们有
然后是尺度变化性质
移位物业:根据这个酒店
现在让我们讨论一些重要的z变换,我将建议读者学习这些变换:
这个函数的拉普拉斯变换是1/s2对应的f(k) = kT。这个函数的z变换是
函数f (t) = t2:拉普拉斯变换这个函数的值是2/s3.对应的f(k) = kT。这个函数的z变换是
这个函数的拉普拉斯变换是1/(s + a)对应的f(k) = e(一种蛋白激酶).这个函数的z变换是
这个函数的拉普拉斯变换是1/(s + a)2对应的f(k) = Te一种蛋白激酶.这个函数的z变换是
这个函数的拉普拉斯变换是a/(s2+ A.2),对应的f(k) = sin(akT)。这个函数的z变换是
这个函数的拉普拉斯变换是s/(s2+ A.2),对应的f(k) = cos(akT)。这个函数的z变换是
现在有时需要再次示出数据,这意味着将离散数据转换为连续形式。我们可以通过下面讨论的HOLD电路将控制系统的数字数据转换为连续形式:
保持电路:这些是将离散数据转换为连续数据或原始数据的电路。现在有两种类型的保持电路,它们被详细解释:
零阶保持电路
零阶保持电路的框图表示如下:
图与零阶保持器有关。
在框图中,我们给了电路一个输入f(t),当我们允许输入信号通过这个电路时,它将输入信号重新转换为连续信号。零级保持电路的输出如下所示。
现在我们有兴趣找出零级保持电路的传递函数。写出输出方程
在以拉普拉斯变换上面的方程我们有
由上式可以计算传递函数为
替代S =Jω,我们可以为零级保持电路绘制Bode图。零级保持电路的电气表示如下所示,其包括与a串联连接的采样器组成电阻器这个组合与一个电阻和的并联组合相连电容器.

相位图-频率响应曲线的ZOH
一阶保持电路
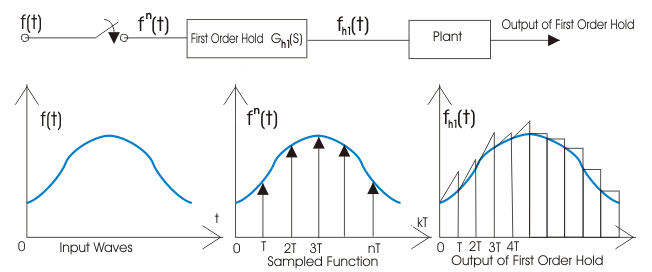
下面给出第一阶保持电路的框图表示:
一阶保持电路
在框图中,我们给了电路一个输入f(t),当我们允许输入信号通过这个电路时,它将输入信号重新转换为连续信号。一阶保持电路的输出如下所示:现在我们感兴趣的是找出一阶保持电路的传递函数。写出输出方程
在以拉普拉斯变换上面的方程我们有
从上面的等式,我们可以计算转移函数(1-E-) / s。代入s=jω,我们可以画出零阶保持电路的伯德图。一阶保持电路的波德图如下所示,它由幅值图和相位角图组成。星等图从星等值2π/ω开始年代.
一阶保持电路的增益图