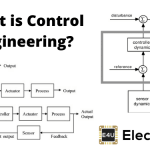
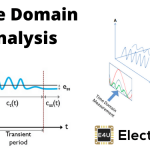
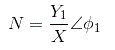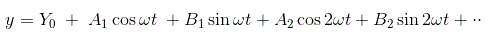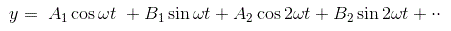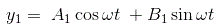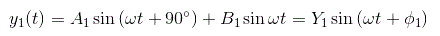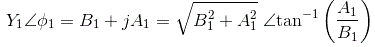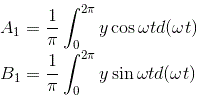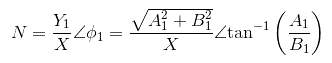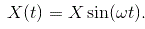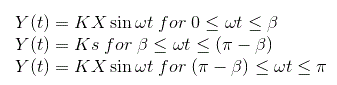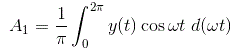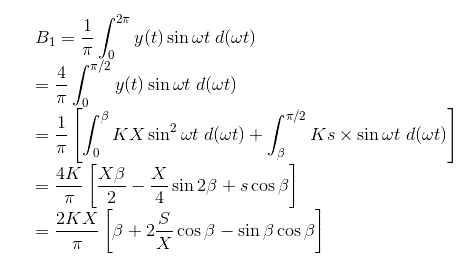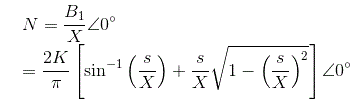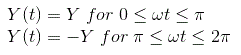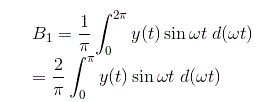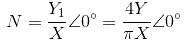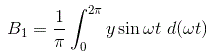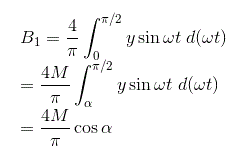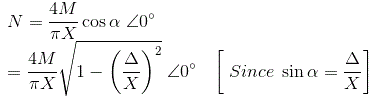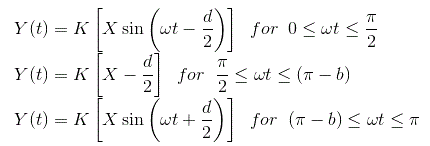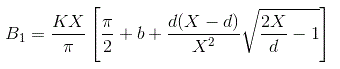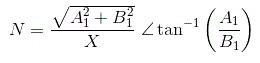这描述功能是分析某些非线性控制问题的近似程序控制工程.首先,让我们回顾一下线性控制系统的基本定义。线性控制系统就是叠加原理(如果两个输入同时被应用,那么输出将是两个输出的和)是适用的。在高度非线性控制系统的情况下,我们不能应用叠加原理。
由于其非线性行为,对不同非线性控制系统的分析非常困难。我们不能使用传统的分析方法,如奈奎斯特稳定性判据或辐射方法以分析这些非线性系统,因为这些方法仅限于线性系统。也就是说,非线性系统有一些优点:
- 非线性系统可以比线性系统更好。
- 非线性系统的成本比线性系统低。
- 与线性系统相比,它们通常尺寸小而紧凑。
在实践中,所有物理系统都有某种形式的非线性。有时,为了提高系统的性能或使其运行更安全,甚至可以有意地引入非线性。结果表明,该系统比线性系统更经济。
一个有故意引入非线性的系统的最简单的例子是继电器控制或ON/OFF系统。例如,在一个典型的家庭供暖系统中,当温度低于某一给定值时,炉子就开启,当温度超过另一给定值时,炉子就关闭。这里我们将讨论分析非线性系统的两种不同的分析或方法。这两种方法写在下面,并在一个示例的帮助下进行简要讨论。
- 描述函数控制系统方法
- 控制系统中的相平面法
共同的非线性
多数情况控制系统类型,我们无法避免某些类型的存在非线性.这些可以分为静态和动态。一个系统的输入和输出之间存在非线性关系,而不涉及微分方程被称为静态非线性。另一方面,输入和输出可以通过一个非线性微分方程联系起来。这样的系统称为动态非线性系统。
现在我们将讨论各种类型的控制系统中的非线性:
- 饱和非线性
- 摩擦非线性
- 死区非线性
- 继电器非线性(开关控制器)
- 强烈的非线性
饱和非线性
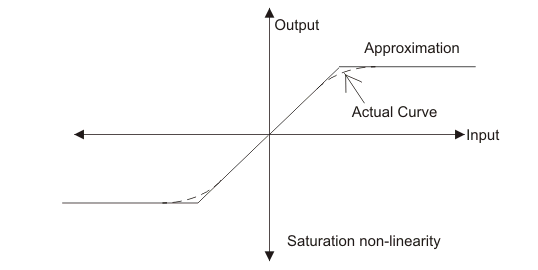
饱和非线性是一种常见的非线性类型。例如,可以看到饱和磁化曲线的非线性直流电机.为了理解这类非线性,让我们讨论饱和曲线或磁化曲线,如下所示:
从上面的曲线我们可以看到,输出显示线性行为在开始,但之后在曲线中有一个饱和,这是一种非线性的系统。我们也给出了近似曲线。
相同类型饱和非线性我们也可以看到,在一个放大器的输出是成比例的输入只有一个有限的范围的输入值。当输入超出这个范围时,输出趋向于非线性。
摩擦非线性
任何反对身体相对运动的东西被称为摩擦。它是系统中存在的一种非线性。一个常见的例子必威电子竞技大赛在其中,我们发现由刷子和换向器之间的摩擦接触而发现库仑摩擦阻力。
摩擦可以分为三种类型,分别表示为:
- 静态摩擦:简单地说,当体静置时,静摩擦在身体上作用。
- 动态摩擦:当物体表面和物体之间有相对运动时,动摩擦作用于物体。
- 限制摩擦:它被定义为在物体静止时作用于其上的极限摩擦力的最大值。
动态摩擦也可以被分类为(a)滑动摩擦(b)滚动摩擦。当两个体彼此滑动时,滑动摩擦是当滚动时滚动时滚动在另一个主体上时。
在机械系统中有两种摩擦即(a)粘性摩擦(b)静摩擦。
死区非线性
死区非线性显示在电机等各种电气设备中,直流伺服电机、执行机构等。死区非线性指当输入超过某一限值时,输出变为零的一种情况。
继电器非线性(开/关控制器)
机电继电器常用于控制策略要求控制信号只有两种或三种状态的控制系统。这也称为开/关控制器或双状态控制器。
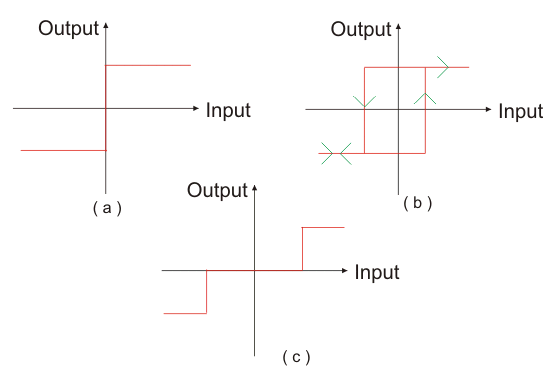
中继非线性(a)开/关(b)开/关用滞后(c)与死区打开/关闭。图(a)示出了双向继电器的理想特性。在实践中,继电器不会瞬间响应。对于两个切换瞬间之间的输入电流,取决于输入的先前历史,继电器可以是一个位置或其他位置。该特性被调用开/关,滞后(B)显示。继电器在实践中,在实践中,在图(c)中的实践中也具有明确的死区。死区是由中继场绕组需要有限量的电流来移动电枢引起的。
反弹非线性
物理系统中常见的另一个重要非线性是机械传动中的迟滞现象,如齿轮系和连杆。这种非线性与磁滞略有不同,通常称为齿隙非线性.齿隙实际上是驱动齿轮和从动齿轮之间的齿隙。考虑如下图(a)所示的齿轮箱,其齿隙如图(b)所示。
图(b)显示了位于齿b中间的从动齿轮的齿A1B2从动档位。图(c)给出了输入和输出运动之间的关系。由于齿A从该位置顺时针驱动,因此在齿A与齿B接触之前,不会发生输出运动1移动距离x/2后从动齿轮的。这一输出运动对应于图(c)中的分段mn。如果假定齿轮传动比为一个单位,则接触后从动齿轮逆时针旋转,旋转角度与驱动齿轮相同。这是由线段no表示的。当输入运动反向时,齿A和齿B之间的接触1是丢失的,从动齿轮立即成为静止的基础上,假设负载是摩擦控制与可忽略的惯性。
因此,当齿A与齿B建立接触后,输出运动使齿A在图(c)所示的相反方向经过分段op移动了一段距离x2,驱动档位现在沿顺时针方向摩擦,如段PQ所示。当输入运动反转时,方向齿轮再次处于段QR的静止,然后沿RN沿驱动齿轮遵循。
非线性系统的函数描述分析
这描述了控制系统中的函数方法是由Nikolay Mitrofanovich Kryloy和Nikolay Bogoliubov在1930年发明的,后来由Ralph Kochenburger发展。
这描述功能方法用于找出在非线性控制系统多年来开发的所有分析方法的非线性系统的稳定性,通常同意最实际上有用的方法。该方法基本上是频率响应方法的近似扩展,包括向非线性系统的奈奎斯特稳定性标准。
这描述功能方法非线性系统的振幅和相位角的复比定义为基波之间的振幅和相位角的复比谐波分量输出到输入正弦。我们也可以称之为正弦描述函数。数学上,
在哪里,
n =描述函数,
X =输入正弦曲线的振幅,
Y =输出的基本谐波分量的幅度,
φ1=输出基谐波分量的相移。
让我们讨论描述非线性控制系统功能的基本概念。
让我们考虑下面的非线性系统的框图,其中g1(s)和g2(s)表示线性单元,N表示非线性单元。
让我们假设输入X到非线性元素是正弦的,即,
对于这个输入,非线性元素的输出y将是一个可以用表示的非正弦周期函数傅里叶级数作为
大多数非线性是奇对称或奇半波对称的;Y的平均值0.对于所有这样的情况为零,因此输出将是,
作为G1(s)g2(s)具有低通特性,可以很好地假设在此过程中滤除了y的所有高次谐波,对非线性元素N的输入x主要由y的基本分量即第一次谐波贡献。所以在描述函数分析中,我们假设只有输出的基谐波分量。由于非线性系统输出的高次谐波的幅值往往小于基次谐波分量的幅值。大多数控制系统是低通滤波器,其结果是高次谐波与基次谐波成分相比大大衰减。
因此,Y.1只需要考虑。
我们可以写y1(t)式中,
在哪里使用量量飞行员,
一个系数1和B1的傅里叶级数由,
从描述函数的定义来看,
让我们找出这些非线性的描述函数。
描述饱和度非线性的函数
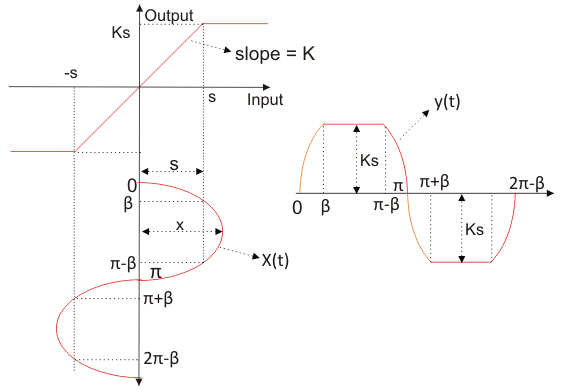
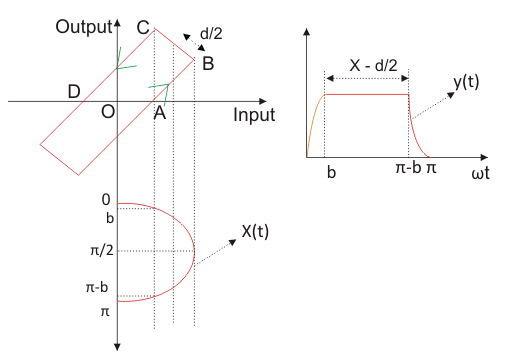
如给定图所示,我们具有饱和度的特征曲线。
让我们采取输入功能
现在我们可以从曲线中定义输出如下:
让我们首先计算傅里叶级数常数1.
将输出值代入上式并对函数从0到2π积分,我们得到常数A1的值为0。
同样我们可以计算傅里叶常数B的值1对于给定的输出和B的值1可以计算为,
描述函数的相位角可计算为
因此,描述饱和度的功能是
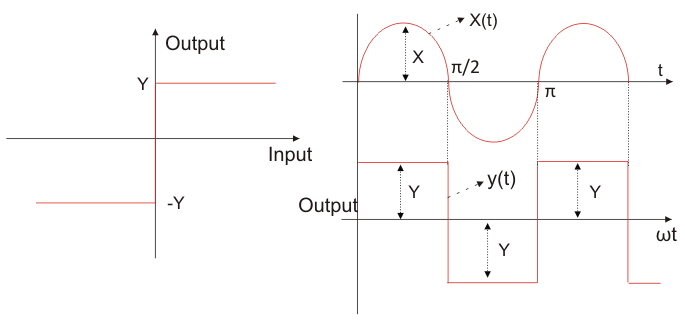
描述理想继电器的功能
我们得到了理想继电器的特性曲线,如图所示。
让我们采取输入功能
现在我们可以从曲线定义输出为
输出周期函数具有奇对称性:
让我们首先计算傅里叶系列常量a1.
将输出值代入上式并对函数从0到2π积分,我们得到常数A的值1为零。
同样我们可以计算傅里叶常数B的值1对于给定的输出和B的值1可以计算为
将输出值代入上式y(t) = y,得到常数B的值1
可以计算描述功能的相位角可以计算为
因此,描述理想继电器的功能是
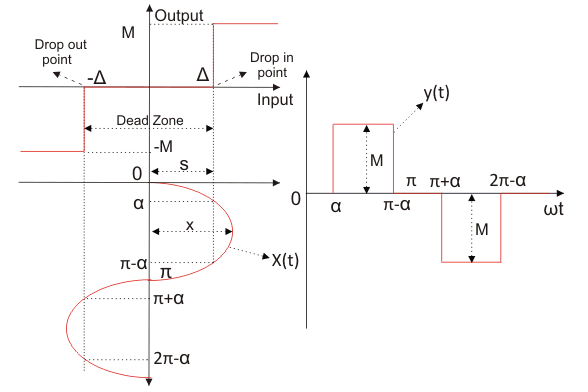
描述真实继电器的功能(有死区继电器)
我们有一个特征曲线,如图所示。如果X小于死区Δ,则继电器不产生输出;的第一个谐波分量傅里叶级数当然是零,描述函数也是零。如果X > Δ继电器产生输出。
让我们采取输入功能
现在我们可以从曲线定义输出为
输出周期函数具有奇对称性:
让我们首先计算傅里叶级数常数1.
将输出值代入上式并对函数从0到2π积分,我们得到常数A的值1为零。
类似地,我们可以计算给定输出的傅里叶常数B的值B的值可以计算为
由于Y的对称性,系数B1可以计算如下:
因此,描述函数为
描述反冲非线性的函数
我们具有曲线的特征曲线,如给定图所示。让我们采取输入功能
现在我们可以从曲线定义输出为
让我们首先计算傅里叶级数常数1.
代替上述等式中的输出的值并将功能从零集成到2π,我们具有常数a的值1作为
类似地,我们可以计算给定输出的傅里叶常数B的值和B的值1可以计算为
代替上述等式中的输出的值并将功能从零集成到PI我们具有常数B的值1作为
我们可以轻松地计算下降方程的基间的描述功能