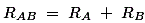电网中的三个分支可以以形式的数量连接,但其中最常见的是星形或三角洲形式。在Delta Connection中,连接了三个分支,它们形成了闭环。由于这三个分支是尾部的鼻子,它们形成了三角形闭环,这种配置称为Delta连接。另一方面,当三个分支的任一末端连接到共同点以形成Y相同的图案被称为星连接。但这些明星和三角洲连接可以从一种形式转换为另一个形式。为了简化复杂网络,三角洲到明星或明星到三角洲转型通常需要。
三角洲到明星转换
通过等效星连接替换Δ或网格被称为三角洲 - 明星转型。如果在任何一条线之间测量阻抗,则两个连接是等同的或彼此相同。这意味着,如果在任何一条线之间测量,则阻抗的值对于不管在线或其等效星之间是否连接到该线之间时,则阻抗在任何一条线之间测量。
考虑一个三角方程组,它有三个角点a B C,如图所示。电阻点A和B,B和C和C和C之间的分支是r1,R.2和R.3.分别。
点A和B之间的电阻将是,
现在,一个星系连接到这些点A,B和C,如图所示。三臂R.一种,R.B.和R.C星形系统分别与A,B和C连接。现在,如果我们测量点A和B之间的电阻值,我们将得到,
由于两个系统是相同的,因此两个系统中的端子A和B之间测量的电阻必须相等。
相似地,抵抗性在两个系统中的点B和C之间相同,
和在两个系统中的点C和相同的电阻,
添加等式(i),(ii)和(iii)我们得到,
从等式(iv)中减去方程(i),(ii)和(iii),
三角星转型的关系可以表达如下。
连接到给定终端的等效恒星电阻等于连接到与相同终端的两个达变电阻的乘积除以Δ连接电阻的总和。
如果Delta连接系统具有相同的抵抗性r在它的三个方面然后等同的恒星抵抗r会是,
明星到三角洲转换
为了星 - 三角洲转型我们只是乘以等式(v),(vi)和(vi),(vii)和(vii),(v),即通过做(v)×(vi)+(vi)×(vii)×(vii)×(v)我们得到,
现在将方程(VIIII)分开(v),(vi)和方程(vii)分开我们得到,