德拉西桥

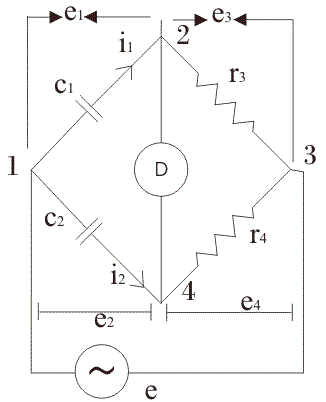
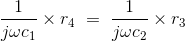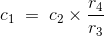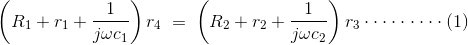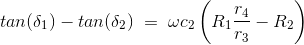该桥为比较两个值提供了最合适的方法电容器如果我们忽略桥接电路中的介电损耗。电路德拉迪的桥梁如下所示。

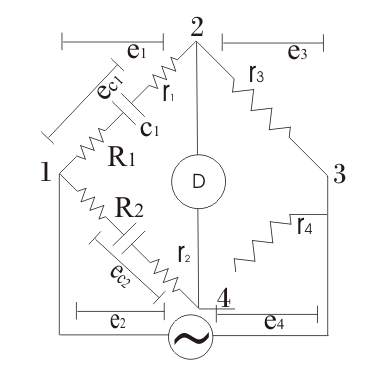
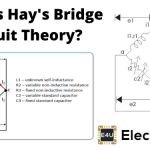
电池在标记为1和4的端子之间施加。臂1-2由电容器C组成₁（其值未知）携带当前的一世₁如图所示，ARM 2-4由纯净组成电阻器（这里的纯电阻器意味着我们假设其在自然界中不感应），臂3-4还由纯电阻器和臂4-1组成，该臂4-1由标准电容组成，其值已经已知为我们。
让我们推导出电容器C的表达式₁就标准电容器和电阻而言。
在平衡条件下，我们有，

它意味着电容器的值由表达式给出

为了获得余额点，我们必须调整r的值_3.或者r._4.没有扰乱桥的任何其他元素。这是比较电容器的两个值的最有效方法，如果所有介电损耗都忽略了电路。

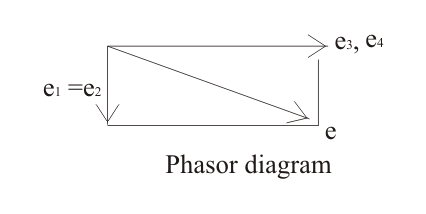
现在让我们绘制并研究这座桥的相位图。Phasor图德拉西桥如下所示：

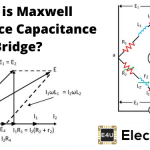
让我们标记当前的丢失在未知电容器上₁那电压下降穿过电阻器_3.是E._3.，臂3-4的电压降是e_4.手臂4-1的电压降是e₂。在平衡状态下，电流流过2-4路径将是零并且电压降低₁和E._3.等于电压降₂和E._4.分别。

为了绘制我们采取的相位图_3.（或E._4.）参考轴，e₁和E.₂以直角显示到e₁（或E.₂）。为什么他们彼此直角？答案这个问题非常简单，因为电容在那里连接，因此获得的相位差角是90^O.。
现在而不是桥梁等一些优点相当简单，提供简单的计算，这座桥的一些缺点是因为这座桥给出了不完美电容的不准确的结果（这里，不完美的电容器不含介电损耗的电容器）。因此，我们只能使用此桥用于比较完美的电容器。
在这里，我们有兴趣修改德拉迪的桥梁，我们希望拥有这样一种桥梁，可以为我们提供精确的电容器的准确结果。此修改由格罗弗完成。修改的电路图如下所示：

这里介绍了格罗弗电阻R.₁和R.₂如上面在臂1-2和4-1上所示，以包括介电损耗。他也有连接的电阻r₁和R.₂分别在臂1-2和4-1中。让我们推导出表达电容器C.₁谁的价值是未知的。我们再次在我们所做的相同臂1-4上连接标准电容德拉迪的桥梁。在等同于电压降的平衡点我们有：

解决上面的等式，我们得到：

这是所需的等式。
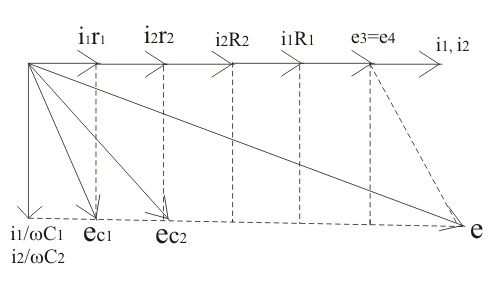
通过制作Phasor图，我们可以计算耗散因子。上述电路的相位图如下所示

让我们标记δ₁和δ₂是电容器的相位角₁和C.₂分别电容器。从Phasor图中我们有Tan（δ₁）=耗散因子=ωc₁R.₁同样我们有了棕褐色（δ₂）=ωc.₂R.₂。
从等式（1）我们有

在乘以ω两侧我们拥有


因此，耗散因子的最终表达被写为

因此，如果已知一个电容器的耗散因子。然而，这种方法对于耗散因子提供了非常不准确的结果。