如何找到一个传递函数的直流增益(包括示例)| Electrical4Ubetway网页版 - betway网页版,betway必威体育精装版,必威亚洲体育

内容

传递函数是什么?

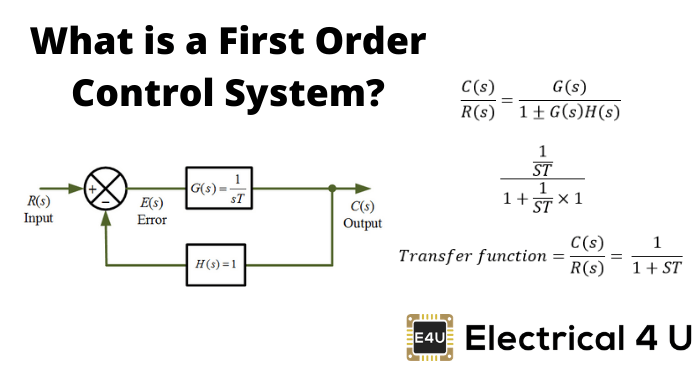
一个转换功能描述了a的输出信号之间的关系控制系统和输入信号。框图是控制系统的可视化，该控制系统使用块来表示表示不同输入和输出信号的传递函数和箭头。

传递函数是线性定常动力系统的一种方便的表示。在数学上，传递函数是一个复变量的函数

对于任何控制系统，都有一个被称为激励或原因的参考输入，它通过传递函数产生一个结果，从而产生一个被控制的输出或响应。

因此，输出和输入之间的原因和效果关系通过传递函数彼此连接。在一个拉普拉斯变换，如果输入表示为 $R (s)$ 输出用 $C (s)$ ．

假设所有初始条件为零，控制系统传输函数被定义为输出变量的拉普拉斯变量转换比到输入变量的拉普拉斯变换。

$\ begin {对齐*} g（s）= \ frac {c（s）} {r（s）} \结束{align *}$

什么是直流收益？

传递函数有许多有用的物理解释。系统的稳态增益就是稳态时的输出和输入的比值，用一个介于负无穷和正无穷之间的实数表示。

当一个稳定的控制系统被一个阶跃输入刺激时，稳定状态下的响应达到一个恒定的水平。

这个词直流收益描述为稳态响应与阶跃输入之间的幅值之比。

DC增益是对稳态步骤的响应的大小与步进输入的大小的比率。这终值定理证明了直流增益是稳定传递函数在0时的传递函数值。

一阶系统的时间响应

动态系统的阶是其控制微分方程的最高导数的阶。一阶系统是最容易分析的动态系统。

为了理解稳态增益或直流增益的概念，考虑一个一般的一阶传递函数。

${对齐*}\开始G (s) = \压裂{G (s)} {R (s)} = \压裂{b_ {0}} {s +现代{0}}{对齐*}\结束$

$G（s）$ 也可以写成

$\ begin {aligne *} \ frac {k} {\ tau s + 1} = \ frac {b_ {0}} {s + a_ {0}} \ end {align *}$

在这里,

$\ begin {align *} a {0} = \ frac {1} {\ tau} \;\;\;\;b {0} = \ frac {k} {\ tau} \结束{align *}$

$\ Tau$ 称为时间常数。K称为直流增益或稳态增益

如何找到传递函数的直流增益

直流增益是系统稳态输出与其恒定输入的比值，即单位阶跃响应的稳态。

为了找到传递函数的直流增益，让我们考虑连续和离散的线性变换逆（LTI）系统。

将连续LTI系统作为

(1） $\ begin {arequation *} g（s）= \ frac {y（s）} {u（s）}} {u（s）} \ neg {arequation *}$

离散LTI系统为

(2） $\开始*}{方程G (z) = \压裂{Y (z)} {U (z)} \{方程*}结束$

利用终值定理计算单位阶跃响应的稳态。

（3) $\{方程*}开始L \离开(y_ (t)}{一步\右)= G (s) \压裂{1}{年代}\{方程*}结束$

（4） $\ begin {等式*} dc \;\;gain = lim_ {t \ lightarrow \ infty} y_ {step（t）} \ end {arequation *}$

（5） ${方程*}直流\ \开始;\;增益= \lim_{s\右箭头0}s\左[G(s)\frac{1}{s} \右]\end{equation*}$

$G（s）$ 是否稳定，所有杆都在左手边

因此，

（6） $\ begin {等式*} dc \;\;gain = \ lim_ {s \ lightarrow 0} s \ left [g（s）\ led] \ neat {arequation *}$

用于连续LTI系统的最终值定理的公式是

（7） ${方程*}\ \开始压裂{y (\ infty)} {u (\ infty)} = G (s) _ {s = 0} = G(0) \{方程*}结束$

用于离散LTI系统的最终值定理的公式为

（8) $\ begin {arearation *} \ frac {y（\ idty）} {u（\ idty）} = g（z）_ {z = 1} = g（1）\ end {equation *}$

在这两种情况下，如果系统有一个集成的结果将是 $\ infty.$ ．

直流增益是稳态输入和稳态输出之间的比值，可以通过对得到的输出进行微分得到稳态导数。对于连续系统和离散系统，这几乎是相同的。

连续域的微分

在连续系统或' s '域中，方程(1)通过将方程乘以' s '来求导。

（9） ${方程*}\ \开始压裂{\点{Y (s)}} {U (s)} = sG (s) \{方程*}结束$

在哪里 $\点{Y (s)}$ 的拉普拉斯变换是什么 $\点{y (t)}$

离散域中的差异化

在离散域的阶导数可以通过一阶差分得到。

（10） $\ begin {arequation *} \ dot {y（k）} = \ frac {y_ {k} -y_ {k-1}} {t} \ neg {arequation *}$

（11） $\ begin {arearation *} \ dot {y（z）} = \ frac {$

(12） $\ begin {arequation *} \ dot {y（z）} = y（z）\ left [\ frac {^ {1-z ^ { - 1}} {t} \ revally] \ neat {arequation *}$

（13） $\开始{方程*}\点{Y (z)} = Y (z) \[\压裂{z 1} {T_ {z}}识别正确\]\{方程*}结束$

因此，要在离散域中求导，我们需要乘 $\ frac {z-1} {t_ {z}}$

数字示例找到DC增益

示例1

考虑连续传递函数，

$\ begin {对齐*} h（s）= \ frac {y（s）} {u（s）} = \ frac {12} {（s + 2）（s + 10）} \ end {align *}$

要找到上述传递函数的直流增益（稳态增益），请应用最终值定理

${对齐*}\ \开始lim_ {t \ rightarrow \ infty} y (t) = \ lim_ {0} \ rightarrow年代\ * \压裂{12}{(s + 2) (s + 10)} \{对齐*}结束$

$\begin{align*}\lim_{t\rightarrow \infty}y(t)= \lim_{s\rightarrow 0}s\times \frac{12}{2\times 3}=2\end{align*}$

现在直流增益定义为稳态值与应用单位阶跃输入的比值。

直流增益= $\压裂{2}{1}= 2$

因此，重要的是要注意，直流增益的概念仅适用于本质上稳定的系统。

示例2

确定方程的直流增益

${对齐*}\开始G (s) = \压裂{K}{\τs + 1} \{对齐*}结束$

上述传输方程的阶跃响应是

$\ begin {aligne *} y_ {step}（t）= l ^ {-1} \ left [\ tauc {k} {（\ tau s + 1）s} \ oft] \ nod {alight *}$

$\ begin {aligne *} y_ {step}（t）= l ^ { - 1} \ left [k \ left（\ frac {1} {s} - \ frac {\ tau} {\ tau s + 1} \右）\右] \结束{align *}$

现在，应用最终值定理来求直流增益。

$\{对齐*}开始y_{党卫军}= \ lim_ {t \ rightarrow \ infty} y_{一步}(t) = \ lim_ {s \ rightarrow 0} \压裂{K}{(\τ+ 1)年代}s = K \{对齐*}结束$