当我们谈到图论中的割集矩阵,我们通常谈论基本割集矩阵.割集是一个分支的最小集合连通图这样,当从图中移除这些分支时,图就会被分成两个不同的部分,称为子图,而割集矩阵是通过逐行每次取一个割集得到的矩阵。的割集矩阵用符号[Qf].
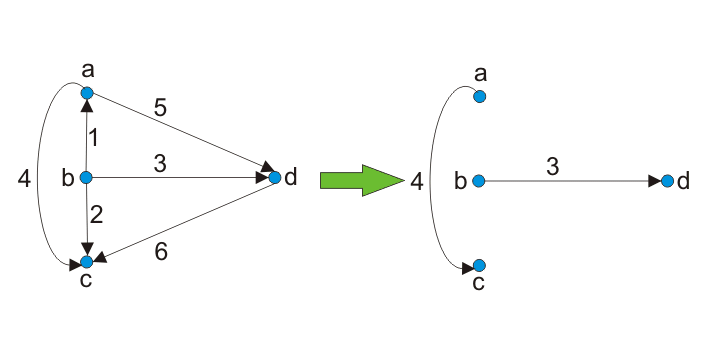
电路的割集矩阵示例
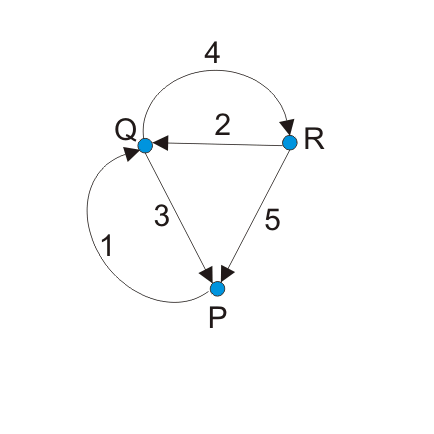
从一个图中选择由分支[1,2,5,6]组成的割集,得到两个子图。
因此,换句话说,我们可以说,给定的参考树的图的基本割集是由一个树枝和剩余的链接组成的割集。细枝是树的分支,链是共树的分支。
因此,截集的数目等于细枝的数目。
[树枝数目= N - 1]
式中,N为给定图或绘制的树的节点数。
割集的方向与树枝的方向相同,取正。
绘制割集矩阵的步骤
有一些步骤应该遵循在绘制割集矩阵.步骤如下-
- 画出给定网络或电路的图(如果给定)。
- 然后画出它的树。这棵树的枝干将变得细小。
- 然后用虚线画出该图的其余分支。这些分支将是链接。
- 树的每一个分枝或小枝将形成一个独立的切块。
- 写矩阵,行作为割集,列作为分支。
| Branchase⇒ | 1 | 2 | 3. | . | . | b | |
| 割集 | |||||||
| C1 | |||||||
| C2 | |||||||
| C3. | |||||||
| . | |||||||
| . | |||||||
| Cn | |||||||
N =割集的个数。
B =分支数。
割集矩阵的方向
问ij= 1;如果分支J在割集中,方向与树枝相同。
问ij= 1;如果分支J在与树分支方向相反的割集中。
问ij= 0;如果分支J不在割集中。
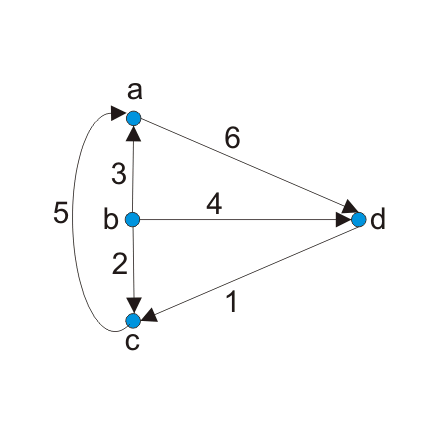
示例1
绘制下图中的割集矩阵。
答:
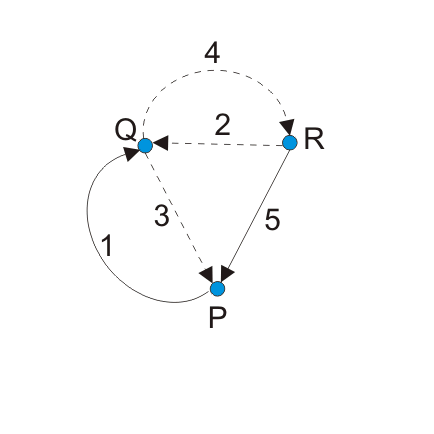
步骤1:画出下图的树。
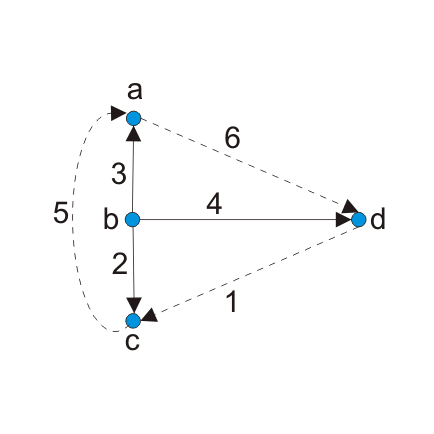
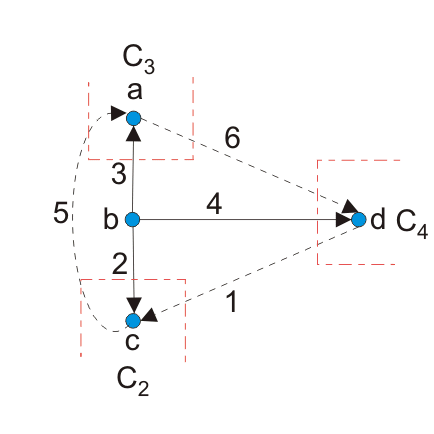
步骤2:现在识别裁剪集。Cut-set将是只包含一个树枝和任意数量的链接的节点。
这里C2C3.和C4割集。
步骤3:现在画出矩阵。
| Branchase⇒ | 1 | 2 | 3. | 4 | 5 | 6 | |
| 割集 | |||||||
| C2 | +1 | +1 | 0 | 0 | -1 | 0 | |
| C3. | 0 | 0 | +1 | 0 | +1 | -1 | |
| C4 | -1 | 0 | 0 | +1 | 0 | +1 | |
这是必需的矩阵。
示例2:
绘制给定图形的割集。
答:
在这个问题中,我们需要重复上一个问题中的步骤。
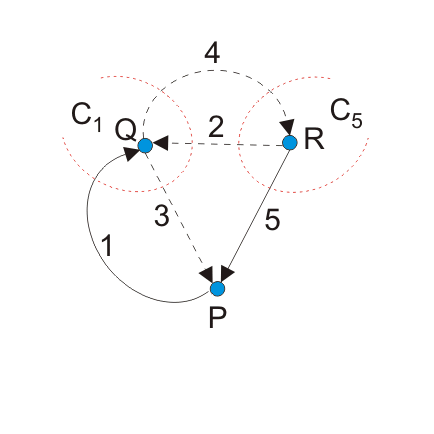
步骤1:画出下图的树。
步骤2:现在识别裁剪集。Cut-set将是只包含一个树枝和任意数量的链接的节点。
这里C1和C5割集。
步骤3:现在画出矩阵。
| Branchase⇒ | 1 | 2 | 3. | 4 | 5 | |
| 割集 | ||||||
| C1 | +1 | +1 | -1 | -1 | 0 | |
| C5 | 0 | -1 | 0 | -1 | +1 | |
这是必需的矩阵。
点要记住
有一些要点是应该记住的。他们是:-
- 在割集矩阵,枝的方向取正。
- 每个剪集只包含一根树枝。
- Cut-set可以有任意数量的链接连接到它。
- 割集矩阵与氯化钾是,