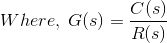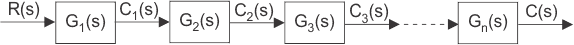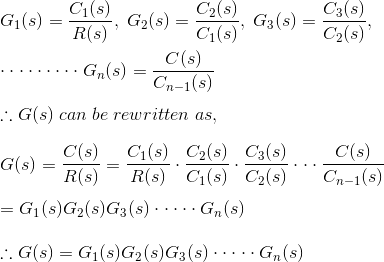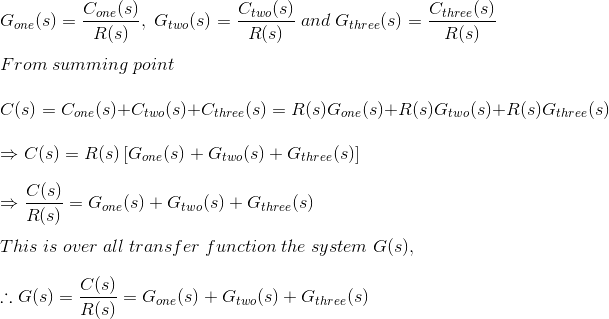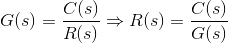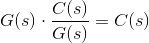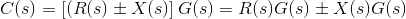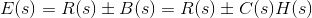内容
什么是控制系统中的框图?
框图用于表示a控制系统以图表形式。换句话说,控制系统的实际表示是其框图。控制系统的每个元素用块表示,块是该元素的传递函数的符号表示。
在单个函数中导出复杂的控制系统的整个传递函数并不总是方便。它更容易分别导出连接到系统的控制元件的传递函数。
然后块表示每个元素的传递函数,然后与路径连接信号流量。
框图用于简化复杂的控制系统。控制系统的每个元素用块表示,并且块是该元素的传送功能的符号表示。完整的控制系统可以用所需数量的互连块表示。
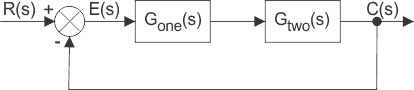
下图显示了两个元素转换功能G一(s)和g二(s)。哪里g一(s)是第一元素和g的传递函数二(s)是系统的第二个元素的传递函数。
该图还示出了存在反馈路径,输出信号C(S)反馈并与输入R进行比较。输入和输出之间的差异是用作致动信号或误差信号。
在图的每个块中,输出和输入通过传递函数与之相关。转移函数是:
其中C(s)是输出,R(s)是该特定块的输入。
复杂的控制系统由几个块组成。每个人都有自己的传递函数。但系统的整体传递函数是最终输出的传递函数与系统初始输入的传递函数的比率。
通过将这些单独的块组合,通过将这些单个块组合,可以通过将控制系统逐一组合来获得该系统的整体传递函数。
组合这些块的技术被称为框图减少技术。
为了成功实施此技术,遵循框图的一些规则要遵循。
让我们一个接一个地讨论这些规则,以减少控制系统框图。如果您正在寻求做一些控制系统学习,请查看我们的控制系统MCQ。
如果控制系统输入的传递函数是R(s)并且相应的输出是C(s),并且控制系统的整体传递函数是g(s),则控制系统可以表示为:
在控制系统框图中取出点
当我们需要向多个块应用一个或相同的输入时,我们使用已知的内容起飞点。
这一点是输入具有多于一个传播路径的位置。请注意,输入不会在某个点划分。
但相反,输入通过连接到该点的所有路径传播,而不会影响其值。
因此,通过具有起飞点,可以将相同的输入信号应用于多于一个系统或块。
表示多个控制系统块的常见输入信号由共同点完成,如下图所示用点X.
级联块
当若干系统或控制块以级联方式连接时,整个系统的传输功能将是所有单个块的传递函数的乘积。
这里还将被记住,任何块的输出都不会受级联系统中其他块的存在影响。
现在,从图中,看来,
其中g(s)是级联控制系统的整体传递函数。
控制系统框图中的求和点
与先前的情况一样,而不是将单个输入信号应用于不同的块,而是可能存在将不同的输入信号应用于同一块的情况。
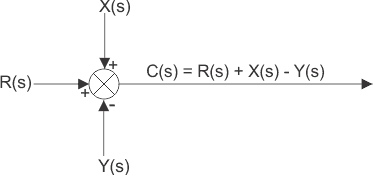
这里,所得到的输入信号是所应用的所有输入信号的求和。输入信号的求和由称为求和点的点表示,如下图所示的圆圈。
这里R(s),x(s)和y是输入信号。有必要指示精细指定输入信号输入求和点控制系统的框图。
连续的总结点
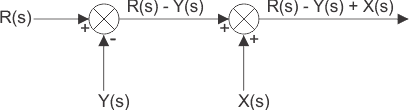
具有两个以上输入的求和点可以分为两个或更多个连续的求和点,其中连续求和点的位置的更改不会影响信号的输出。
换句话说 - 如果有一个以上的总和直接相关联,则它们可以容易地从其位置互换,而不会影响求和系统的最终输出。
平行块
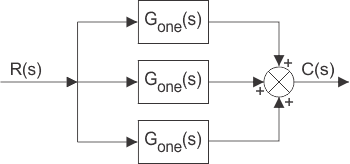
当应用相同的输入信号时,在求解系统最终输出的求和点中添加不同的块和来自它们中的每一个的输出。
系统的整体传递函数将是所有单个块的传递函数的代数总和。
如果是C.一, C二,和c三是带传递函数g的块输出一, G二,和G.三, 然后。
转移起飞点
如果将相同的信号应用于多于一个系统,则信号在系统中表示称为耗时点的点。
原则转移起飞点是它可以在块的任一侧移动,但是必须未改变连接到起飞点的分支的最终输出。
起飞点可以转移到块的任一侧。
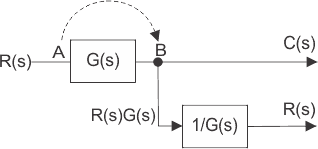
在上图中,取出点从位置A转移到B.在点B时熄火点A的信号R(S)将变为G(S)R.
因此,另一个转移函数g的逆块将被放置在该路径上以再次获得r(s)。
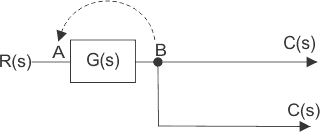
现在让我们在块之前转移到块之前的截止点,这是在块之后的。
这里输出是C(s),并且输入是r(s),因此。
在这里,我们必须在路径上放置一个传输函数g(s),以便再次输出为C(s)。
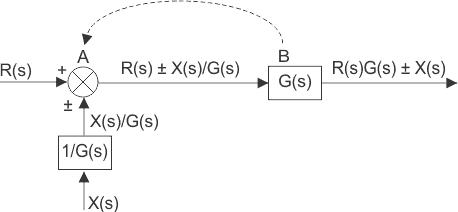
转移求和点
让我们在块之后的块之前从一个位置检查求和点。
有两个输入信号,R(s)和±x(s),在位置A的求和点中输入。求和点的输出是R(S)±x(s)。
所得到的信号是控制系统转移函数G(s)块的输入,并且系统的最终输出是
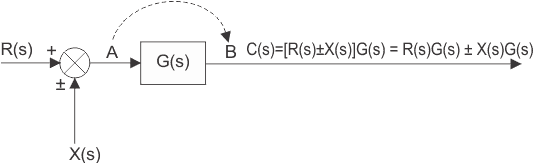
因此,可以用输入信号R(s)g(s)和±x(s)重新绘制求和点
上述控制系统输出的框图可以重写为
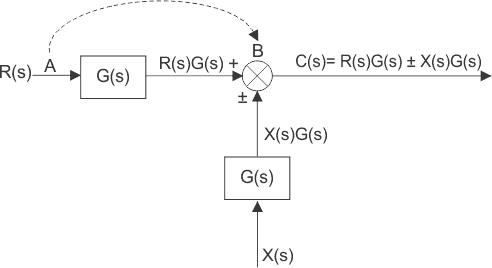
上述等式可以由转移函数G块表示,并再次表示R(s)±x(s)/ g(s)可以表示的r(s)±x(s)/ g(s)具有输入信号R(s)和±x(s)/ g(s)的求和点,最后可以如下绘制。
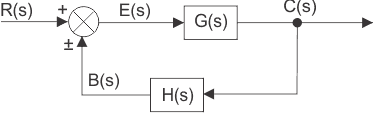
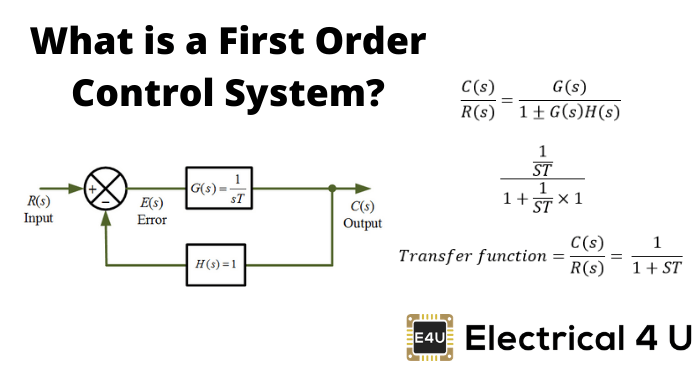
闭环控制系统框图
在一个闭环控制系统,一部分输出被送回并添加到系统的输入中。如果h(s)是反馈路径的传递函数,则反馈信号的传递函数将是b(s)= c(s)h(s)。
在求和点,输入信号R将被添加到B(s)并产生系统的实际输入信号或误差信号,并且它由e表示。