格雷码：二进制到灰色码转换器

什么是格雷码?

灰色代码- 也被称为循环代码那反映二进制编码（RBC），反映二元（rb）或灰色代码- 被定义为二进制数字系统的排序，使得每个增量值只能不同。在灰色代码中，在代码组中仅遍历一步到另一步，只有一位更改。也就是说，两个相邻的代码仅不同于一位彼此不同。

格雷码是单位距离代码中最流行的，但它不适用于算术运算。格雷码在模拟转换器中具有一些应用，以及用于数字通信中的纠错。灰色代码最初可能难以理解，但在查看下面的灰色代码表时变得更加容易理解。

灰色代码表

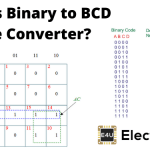
表显示二进制代码与灰色代码和十进制到格雷码之间的转换的表如下：

二进制到灰色码转换器

将二进制代码转换为等效变灰代码的逻辑电路已知为二进制到灰色码转换器。可以通过在2之后反映轴的N-1位代码来获得n比特格雷格码^N-1行和将轴上的0上方的MSB（最高有效位）和轴下方的1的MSB放置。灰度码的反射如下所示。

下面给出了4位二进制码转换表：

这意味着，在4位格雷码中，（4-1）或3位代码反映在（2^4-1）^TH.或8.^TH.排。

二进制到灰码转换电路如下所示：

如何将二进制文件转换为灰色代码

1. MSB（最高有效位）的格雷代码将与给定二进制数的第一位完全相同。
2. 代码的第二位将是给定二进制数的第一和第二位的排他性 - 或（xor），即，如果两个比特都相同，结果将是0，如果它们不同，结果将是1。
3. 灰码的第三位将等于给定二进制数的第二和第三位的异或(XOR)。这样二进制到灰码的转换就进行了。下面给出一个示例来说明这些步骤。

二进制到格雷码转换示例

假设我们有一个二进制数字01001，我们希望转换为灰色代码。让我们通过我们将如何执行此转换的示例：

1. MSB保持不变。由于二进制的MSB为0，但是灰色码的MSB也是0（第一灰度位）
2. 接下来，拍摄第一和第二二进制比特的XOR。第一位为0，第二位为1.位是不同的，所以所得到的灰度位为1（第二灰度位）
3. 接下来，拍摄第二和第三二进制位的XOR。第二位为1，第三位为0.这些位再次不同，因此所得到的灰度位为1（第三灰度位）
4. 接下来，拍摄第三和第四二进制比特的XOR。第三位为0，第四位为0.因为它们相同，所得到的灰度位为0（第四灰度位）
5. 最后，取出第四和第五二进制比特的XOR。第四位为0，第五位为1.这些位是不同的，因此得到的灰度位为1（第五灰度位）
6. 因此01001的二进位灰码转换结果是完整的，等效灰码为01101。

灰色到二进制代码转换器

在一个灰度到二进制码转换器，输入为灰色代码，输出是其等效二进制代码。

让我们考虑一个4位的灰度到二进制代码转换器。为了设计一个4位灰二进制码转换器，我们首先要绘制一个灰码转换表，如下图所示:

到二进制转换器电路的灰度代码如下所示：

到二进制转换的灰色代码

到二进制转换的灰色代码再次是一个非常简单和简单的过程。以下步骤可以使您的想法在这种转换中明确。

1. 二进制数的MSB将等于给定灰码的MSB。
2. 现在，如果第二灰度位为0，则第二二进制位将与前一个或第一位相同。如果灰度位为1，则第二二进制位将改变。如果是1，它将是0，如果是0，那将是1。
3. 所有比特都继续执行此步骤到二进制转换的灰色代码。

下面给出的一个例子将使您的想法明确。

二进制转换示例的格雷代码

二进制的MSB将为0，因为灰色的MSB为0.现在移动到下一个灰度位。由于它是1个前一个二进制比特将改变I.E将是1，因此第二二进制比特将是1.下一步看看灰色码的第三位。It is again 1 thus the previous bit i.e the second binary bit will again alter and the third bit of the binary number will be 0. Now, the 4th bit of the given gray is 0 so the previous binary bit will be unchanged, i.e 4th binary bit will be 0. Now again the 5th grey bit is 1 thus the previous binary bit will alter, it will be 1 from 0. Therefore the equivalent binary number in case of gray code to the binary conversion will be (01001).

灰色代码示例序列

1. 格雷代码只能将一位从其上一步更改为下一步。位的变化始终从右侧到左侧的左侧发生，即从LSB（最低有效位）朝向MSB（最有效位）。
2. 我们知道，对于二进制数字，有两种可能的组合 - 0和1.遵循我们的规则，我们首先瞄准LSB（右侧）。因此，前三个比特保持恒定（即000），并且第四位从0变为1.这是1的十进制等效项。
3. 现在从LSB i.e.e.s移动到下一位。第3位。我们现在将该位从0变为1，这是2（0011）的十进制等效物。请注意，与二进制不同，我们不能从0001到0010转到，因为这同时改变第3位（0到1）和第4位（1到0）。
4. 现在从0011增加，我们从LSB（右侧）开始，并注意到我们到目前为止还没有看到组合0010。因此，我们将前三个位保持常量，并将最后一位从1变为0.因此，十进制数3的格雷代码是0010
5. 遍历下一个代码。我们不能更改第3个或第4位，因为我们之前看到这些组合。因此，我们将其移至第二位并从0到1的变化。这在格雷码中给出了十进制数4。您可能会质疑为什么我们不能再次更改第三位，这也将是前一个的单位变化。但是随着第三位改变，给出前面发生的等效变灰0000（十进制数0），我们不能这样做。请记住，先前无法重复发生的数字。
6. 重复先前的步骤，我们将保持第一和第二位常量，并通过仅在每个步骤中仅在每个步骤中更改1位，找到第三和第四位的可能组合。从第4位开始，因为这是LSB。

4位格雷码的位被视为g_4.G_3.G₂G₁。现在来自转换表，

从上面的sops（产品的总和），让我们画画卡诺酱地图（k映射）g_4.， G_3.， G_2，和G.₁。

灰色代码的应用

格雷码用于少数特定应用程序。主要应用包括用于模拟到数字转换器，以及用于数字通信中的纠错。灰色代码用于最小化将模拟信号转换为数字信号的误差。

弗兰克灰色 - 灰色代码被命名为后 - 专利了脉冲代码调制（PCM）管。这种PCM管由雷蒙德W.贝尔实验室的西尔斯制成（与Frank Gray和William M. Goodall一起使用），他归功于反映二进制代码的想法（即灰色代码）。你可以读到这一点通过脉冲代码调制电视。

格雷码的其他一些应用：

• 布尔电路最小化
• 时钟域之间的通信
• 纠错
• 遗传算法
• 数学谜题
• 位置编码器

灰色代码的优点

• 更好地在将模拟信号转换为数字信号时更好地最小化
• 在使用时减少了“汉明墙”（不期望的状态）的发生遗传算法
• 可用于最小化逻辑电路
• 用于时钟域交叉

灰色码的缺点

• 不适用于算术运算
• 在几种特定应用外面的实际使用有限