我们主要熟悉的数字系统是十进制数字系统。十进制数字系统具有十个基础,暗示有十个数字,我们可以代表任何数量的十进制家庭。这些数字为0到9.表示是(15)10基座10被写为后缀或基数。如果没有写入,那么默认情况下必须明白它是默认情况下的十进制数字。
另一方面,戈特弗里德·莱布尼茨(Gottfried Leibniz)在1679年发明的二进制数以2为底。“Bi”的意思是二,因此我们可以说二进制的底数是2。也就是说,只有两个数字就足以用二进制格式表示一个数字。二进制数系统中使用的数字是0和1。
二进制数可以在表示基数的前缀中加上2来表示。如果没有给出基数,则默认为十进制数。我们在写二进制数时必须非常小心,一个小错误可能会导致一个非常严重的错误。例如,一个二进制数写为(00110)2.
现在可能出现一个问题,为什么我们需要二进制数?我们拥有十进制数字系统,熟悉我们所有人,大多数人都不理解二进制。答案是任何可编程设备或处理器都可以在高或低的两种模式下工作。
这里,高表示电源连接到该点,低表示该点接地或处于零伏状态。这被称为正逻辑,在其他逻辑系统中采取相反的被称为负逻辑系统。
我们还可以说,高表示执行了某些功能或工作,低表示没有执行任何工作。如果我们采用否定的逻辑系统,情况也可能相反。
所以,从上面的描述我们可以说,它是更容易和方便的使用二进制数字系统在计算机中,为了用户的需要,需要将以二进制形式给出的输出结果转换为十进制,而不是十进制。
二到十进位转换
整数的转换
就像你一样将任何二进制数转换为十六进制,或将二进制数转换为八进制数,任何二进制数都可以转换成十六进制数。
这种转换也是很简单的方法。设,一个二进制数为(11010)2,其中从最高有效位开始的二进制数的权值为24, 23., 22, 21, 20分别。
现在这些位乘以它们的权值,这些乘积的和就是各自的十进制数。现在让我们按照以下数学步骤来做:
因此,(26)10是所需的十进制数。这是如何执行二进制转换的二进制转换。
作为另一个例子,我们转换二进制数(1110)2到十进制数:
转换二进制数到十进制数
小数点到小数的转换
这也可以以相同的方式完成,但是在小数点之后,数量应该乘以2-1, 2-2等。
例如,
十进制到二进制转换
整数十进制数到二进制
将这个数除以2,然后只取余数,如果除法完成,则只取给出二进制数的余数。
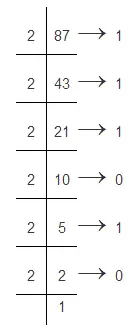
假设我们在转换十进制数(87)10.我们将87划分为2,并获得43作为商品,1作为其余部分。如下所示,这些剩余物写在旁边。
余数的可能性(87)10= (1010111)2只有1和0。因此,从最后一个余数开始计算。如1→0→1→0→1→1→这就是如何十进制到二进制转换就完成了。
分数十进制数到二进制
在这种情况下,逐次乘法就完成了。要转换的数字与二进制数的基数2相乘。把整数部分或者乘积的进位取出,重复同样的过程,直到我们得到一个整数。例如,
二进制等同物(.95)10评估如下-
由于我们在连续的乘法之后并没有得到整数值,所以我们可以将其近似为(.111110....)2.
从负十进制到二进制
如果是负数,我们可以取2的补有符号数的表示。
示例- 9 = 0000 1001
1的补充0110 = 1111。
加1得到11110111这是2的补码表示(-9)