二进制减法器

在讨论之前二进制子信制，让我们讨论减去两个多位的方法二进制数字。

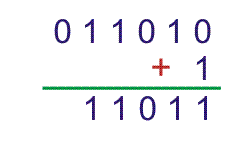
对于上面的减法，我们使用了一般的规则，

借1，然后加到第一个二进制数的下一个高有效位上。然后，第二个二进制数的相同位置将被减去。

但是还有其他方法可以自信地减去两个二进制数。其中一个是2的补充脱基质的方法。

这里，第一二进制数（从哪个要减去的二进制数）被保留，如图所示。然后补充，然后补充第二二进制数（要对其进行减去）。然后将1添加到补充的第二二进制数的LSB。结果2的第二个二进制数的补充。现在，我们最后添加了第一个二进制数，2的第二个二进制数的补充，我们得到了解除减轻的最终结果。
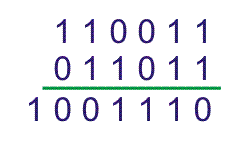
在前面的例子中，
第一的二进制数是110011，第二二进制数为100101。补充或1的补100101是011010.现在通过添加1的LSB，我们得到的补充号码的LSB，

现在通过添加第一个数字，110011和2的补充第二个数字，即11011。我们得到,

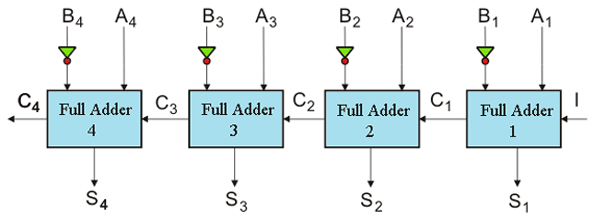
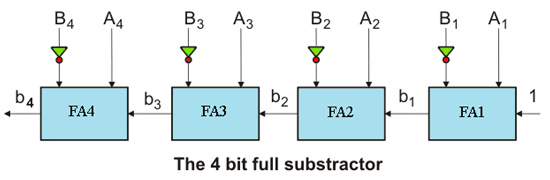
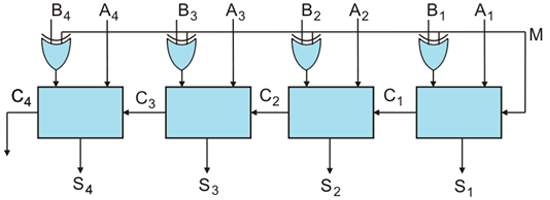
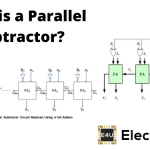
因此，4位减法器可以这样画:

在这里，答：_4.， 一种_3.， 一种₂， 一种₁是minuend和b_4.，B._3.，B.₂，B.₁是分层。S._4.，S._3.，S.₂，S.₁是下划线的结果_4.是最终的携带，忽略了这一点。

半次次次次子

半次次次次子是一个组合电路，其执行单比特二进制数的子分子。两个单位二进制数的后退组合可以是，

现在，如果我们画一个真相表为此，通过所有差异（d）和借用（b），我们得到，

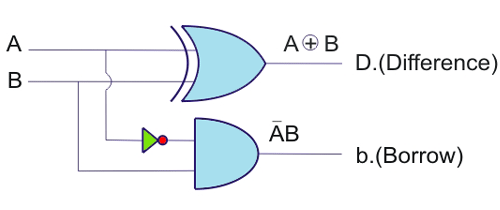
因此，从真相表找到了，

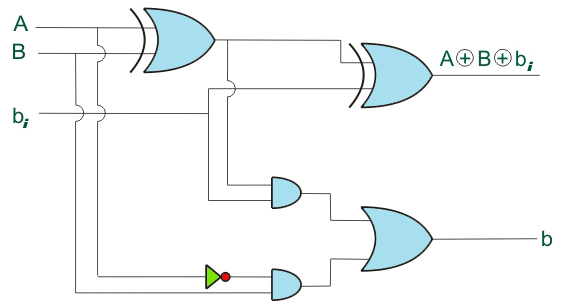
可以使用逻辑门来表示上述等式。

上述电路是逻辑半亚基电路。

完整的子系统

这对于仅在两个单位二进制数之间执行子系统是不实际的。相反，二进制数始终是多维数据。从右（LSB）向左（MSB）进行两个二进制数的逐位进行比特。在同一重要位和子系统的分布过程中，可能有一个借用差异位。此借用位（0或1）将被添加到下一个更高的Minuend中，然后从此中减去下面的子系统的下一个相应的位。它将继续到MSB。组合逻辑电路执行此操作被调用满substractor。因此，完整的子系统类似于半子变量，但完整的子系统中的输入是三个而不是两个。
两个输入是为减数位和减数位，第三个输入是为从前面的位减法借来的。全加法器的输出与半加法器的输出相似，分别是差(D)和借(b)。

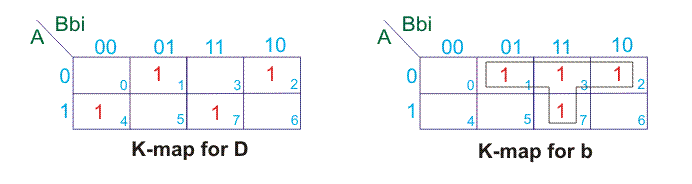
Minuend位（a），subtrahend位（b）和输入借用（bi）及其各自的差异（d）和输出借伯罗（b）的组合在a中表示真相表,遵循

让我们画画K-map对于d和b。

二进制加法器子系统

我们已经设计了4位二进制并行加法器和4位二进制子信制。还可以看出，除了子句子之外，两个电路除了子系统中，子系统中位输入与LSB的输入借款位是1的。


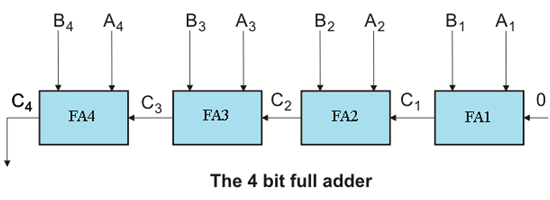
在上述4位全加法器电路中，第三个输入到LSB加法器（FAI）是1.除此之外，在完整的子系统处于不可甲板，即B.₁，B.₂，B._3.和B._4.是反向的。
我们可以通过控制B将这两个电路（加法器和子系统）组合在一个电路中。₁，B.₂，B._3.和B._4.LSB加法器单元（FAI）的终端和第三输入。我们知道，

所以，我们可以使用XOR门在每个输入b₁，B.₂，B._3.和B._4.使用控制输入M（1或0）。
现在，如果m = 1，b₁，B.₂，B._3.和B._4.将补充。同时当FAI的第三输入为1时，电路成为减法电路。因此，M = 1也被馈送给减法中FAI的第三个输入。